Постановка диагноза по комплексу диагностических параметров.

Из врачебной практики и опыта технической диагностики диагноз, как правило, ставится не по одному, а по нескольким признакам. При анализе совокупности симптомов у диагноста интуитивно возникает «догадка» о наиболее вероятном диагнозе. Чем глубже знания и больше опыт диагноста, тем достовернее выдвигаемый им диагноз.

При разработке системы автоматической диагностики необходимо располагать алгоритмом постановки диагноза, на основании которого может действовать некоторая схема (в общем случае – ЭВМ)

При изменении технического состояния автомобиля различные неисправности могут частично сопровождаться одинаковыми диагностическими параметрами. Например, не герметичность клапана поплавковой камеры карбюратора ( 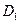) сопровождается: повышенным расходом топлива - 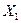, перегревом двигателя - 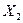, большим содержанием СО в выхлопных газах - 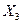, загрязнением карбюратора - 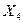. Износ топливных жиклеров ( 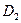) сопровождается: повышенным расходом топлива - 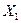, перегревом двигателя - 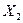, большим содержанием СО в выхлопных газах - 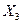. Неправильная регулировка холостого хода ( 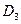) сопровождается указанными ранее признаками 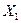, 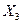и неустойчивой работой двигателя на холостом ходу - .

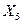Описание диагнозов удобно свести в матрицу, обозначая наличие признака «1», а отсутствие – «0» (Таблица 1)

Таблица 1.

Диагнозы	Диагностические параметры

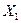
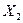
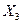
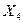
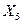
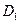
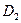
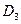
На основании подобных матриц делались попытки создавать электрические приборы для автоматической постановки диагнозов, содержащие набор тумблеров (включателей) и сигнальных лампочек (по числу диагнозов). При соответствующем строке диагноза сочетании включенных и выключенных тумблеров в приборе зажигается лампочка данного диагноза. Однако, на практике такие приборы оказались неработоспособные, что объясняется следующим образом.

Как уже отмечалось ранее, контролируемые диагностические параметры имеют случайный разброс из-за ошибок измерения, случайного сочетания режимов работы разных элементов автомобиля и т. п. Поэтому наличие или отсутствие диагностического признака при определенном диагнозе 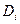не является достоверным событием («1» или «0»), а наблюдается с некоторой условной вероятностью .

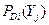Наблюдая за большой группой автомобилей можно установить, как часто встречаются интересующие нас диагнозы - 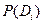, и с какой вероятностью при этих диагнозах встречаются принятые для разрабатываемой системы диагностические параметры - 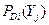. Для определения вероятностей наблюдения различных признаков, можно искусственно вносить в автомобиль интересующие нас неисправности (нарушать регулировки и т. п.).

Пусть результаты статистических исследований по ранее рассматриваемому примеру будут представлены таблицей 9.

Поскольку используется вероятностный подход, то к трем рассматриваемым в табл. 1 диагнозам, в табл. 2 прибавлен еще один, образующий полную группу событий, диагноз 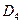- все остальное, т. е. все возможные другие неисправности.

Таблица 2.

Диагноз	Вероятности диагностических параметров	Вер. диагноза
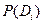
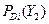
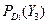
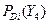
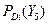
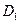
	1,0	0,8	0,9	1,0	0,2	0,05
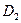
	0,9	0,7	0,9	0,0	0,2	0,10
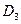
	0,6	0,1	0,9	0,1	0,9	0,30
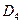
	0,1	9,1	0,0	0,1	0,0	0,55

Поставим диагноз для автомобиля с комплексом признаков: двигатель перерасходует топливо - 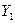, перегревается - 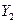, карбюратор грязный - 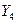, остальные диагностические параметры не наблюдаются, т. е.

.

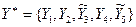Расчет наиболее вероятного диагноза можно произвести по известной в теории вероятностей формуле Бейеса, рассмотрим ее типичный вывод.

Пусть в урне находится 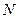шаров, среди которых 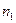- пустотелые, из них 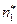- белые, и 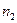- сплошные, из них 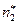- белые (остальные пустотелые и сплошные шары черные).

Вероятность вынуть пустотелый шар (события )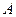

.

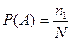Вероятность вынуть белый шар (события )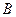

.

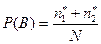Вероятность, что вынутый пустотелый шар окажется белым,

.

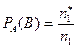Вероятность, что вынутый белый шар окажется пустотелым,

.

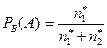Вероятность, что шар будет белым и пустотелым (совместное наблюдение двух событий определяется произведением вероятностей)

.

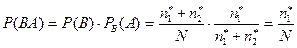Вероятность, что шар будет пустотелым и белым

.

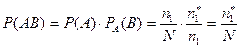Поскольку 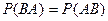, можно записать

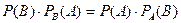, отсюда формула Бейеса

.

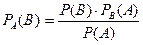Применительно к диагностике формулу Бейеса можно записать

,

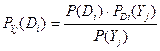где 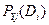- вероятность 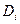- го диагноза при наблюдении 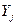-го параметра;

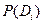- вероятность 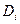- го диагноза;

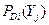- вероятность наблюдения 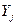- го параметра при диагнозе ;

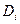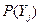- вероятность наблюдения 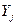- го параметра по всем диагнозам.

Поясним записанную формулу наглядным примером. К врачу на прием пришел больной с высокой температурой. С какой вероятностью у больного грипп? Если в данный момент в городе наблюдается эпидемия гриппа, то вероятность этого диагноза велика. Если данный вирус не сопровождается высокой температурой, то это снижает вероятность постановки диагноза – грипп. Если в поликлинику практически все приходят с высокой температурой (знаменатель формулы велик), то это тоже снижает вероятность постановки диагноза – грипп.

При постановке диагноза по комплексу признаков, формула будет записываться аналогично, но вместо единичного параметра 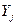будет рассматриваться комплекс параметров .

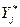Вероятность совместного наблюдения независимых признаков, составляющих анализируемый комплекс диагностических параметров, можно выразить произведением вероятностей наблюдения каждого параметра при рассматриваемом диагнозе 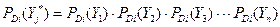. Если в комплексе некоторые признаки отсутствуют, то в произведение ставят вероятность отсутствия диагностического параметра .

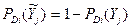Вероятность наблюдения комплекса признаков по всем диагнозам определяют по формуле полной вероятности (как математическое ожидание)

.

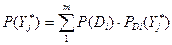Используя данные табл. 9, рассчитаем вероятности диагнозов для заданного ранее комплекса диагностических параметров .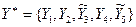

.

.

.

.

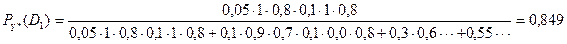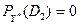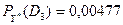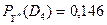На основе проведенных расчетов можно сказать, что для автомобиля с набором признаков, соответствующих заданному комплексу диагностических параметров, наиболее вероятным является первый диагноз: негерметичен запорный клапан поплавковой камеры карбюратора. Практически невероятен износ жиклеров, мало вероятно, что у карбюратора не отрегулирована система холостого хода. Если первый диагноз не подтвердится при проверке карбюратора, то вторым по значимости будет четвертый диагноз: причина плохой работы двигателя кроется в чем-то другом.

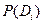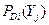Естественно, что в реальных системах диагностирования подобные расчеты должны проводиться микропроцессорной схемой автоматически. Система диагностирования должна предусматривать процесс «обучения», т. е. корректирования матрицы вероятностей по мере накопления опытных данных. С этой целью в памяти ЭВМ следует хранить не только вероятности и , но и общее число объектов 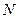, по которым определялись вероятности диагнозов 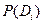, а также 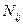- число объектов с признаком 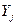при диагнозе .

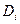Если поступает новый объект с диагнозом 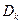, то проводят корректировку прежних априорных вероятностей следующим образом:

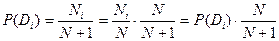для , ;

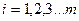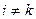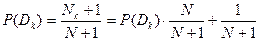при .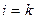

После этого присваивается новое значение числу объектов .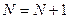

Корректировку вероятностей признаков проводят только для строки с диагнозом 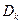следующим образом:

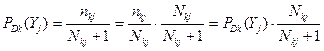, если признак 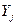у нового объекта отсутствует;

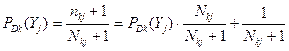, если признак 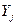у нового объекта присутствует.

В этих расчетах 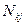- общее число объектов, по которым рассчитывалась вероятность наблюдения признака; 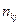- число объектов, у которых признак 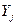наблюдался.

Таким образом, после диагностирования очередного автомобиля и подтверждения фактического диагноза по результатам разборки узла или каким либо другим образом, диагност вносит коррективы в диагностическую матрицу. В результате такой процедуры диагностическая система «обучается», «набирается опыта», что имитирует рост профессионального мастерства человека, занимающегося диагностированием.

Л6