Оценка безотказности сложных систем.
В зависимости от характера влияния на надежность сложной системы, ее элементы можно считать включенными последовательно или параллельно (по аналогии с включением лампочек в гирлянде). При этом реальную конструктивную схему системы следует представлять структурной схемой безотказности. Приведем пример структурной схемы подшипникового узла, состоящего из следующих элементов: 1 – вал, 2 – подшипник, 3 – корпус подшипника, 4 – винты крепления крышки подшипника (4 шт.), 5 – крышка подшипника. Если отказ элемента приводит к отказу системы, то можно считать, что элемент включен последовательно. Если при отказе элемента система продолжает функционировать, то элемент включен параллельно. В соответствие с этим структурная схема подшипникового узла будет иметь вид рис. 19.
 |



| |
| |
| |
| |









| |
| |
| |


Рис. 19.
Безотказность сложной системы, состоящей из последовательно включенных элементов, определяется произведением вероятностей безотказной работы элементов 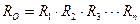 =
= 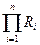 . Например, система состоит из 50-и элементов с одинаковой безотказностью
. Например, система состоит из 50-и элементов с одинаковой безотказностью 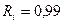 , то
, то  .
.
Как видно из приведенного примера, увеличение элементов при их последовательном включении приводит к снижению безотказности сложной системы.
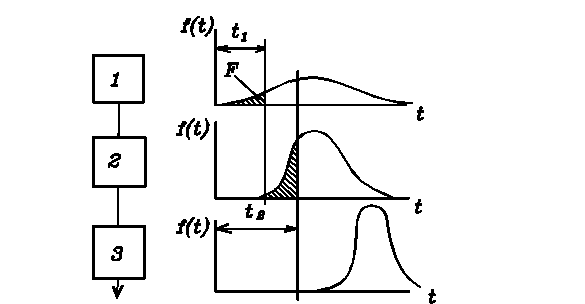 |
Для реальных элементов безотказность является переменной величиной, зависящей от их наработки, ее можно выразить законом распределения вероятностей. На рис. 20 показаны графики законов распределения вероятностей для трех последовательно включенных элементов.
Рис. 20.
Из графика следует, что при наработке 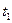 наибольшую вероятность отказа
наибольшую вероятность отказа 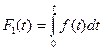 будет иметь первый элемент, однако, при увеличении наработки до величины
будет иметь первый элемент, однако, при увеличении наработки до величины 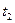 вероятность отказа второго элемента может существенно возрасти. Третий элемент при рассматриваемых значениях наработки остается, практически, безотказным. Таким образом, для повышения безотказности системы, состоящей из последовательно включенных элементов, следует в первую очередь повышать надежность наиболее «слабых» элементов. Одинаково увеличивать средний ресурс всех элементов системы нецелесообразно.
вероятность отказа второго элемента может существенно возрасти. Третий элемент при рассматриваемых значениях наработки остается, практически, безотказным. Таким образом, для повышения безотказности системы, состоящей из последовательно включенных элементов, следует в первую очередь повышать надежность наиболее «слабых» элементов. Одинаково увеличивать средний ресурс всех элементов системы нецелесообразно.
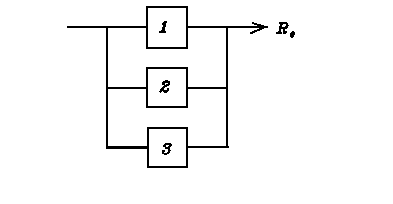 |
При параллельном включении элементов (рис. 21) сложная система откажет только при отказе всех
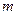 элементов, вероятность этого события
элементов, вероятность этого события  . Безотказность сложной системы
. Безотказность сложной системы 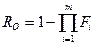 , или
, или 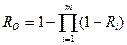 .
.
Рис. 21.
Например, для системы из трех элементов с безотказностью 0,9 общая безотказность 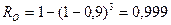 . Таким образом, увеличение числа параллельно включенных элементов увеличивает безотказность сложной системы.
. Таким образом, увеличение числа параллельно включенных элементов увеличивает безотказность сложной системы.
Л8
Дата добавления: 2015-08-14; просмотров: 1479;
