Долговечности изделий.

Рис. 23.

Если в рассматриваемом примере безотказность фильтра по прорыву фильтрующего элемента 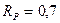, а по забиванию - 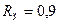, то при параллельном включении фильтров общая безотказность по прорыву будет равна 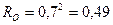, а по забиванию - 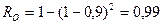. При последовательном включении фильтров общая безотказность по прорыву 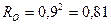, а по забиванию 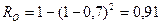. Сравнивая минимальные значения общей безотказности, можно сделать вывод, что при последовательном включении фильтров рассматриваемая сложная схема надежнее. (Не следует забывать, что этот вывод справедлив при заданных значениях безотказности по рассматриваемым параметрам).

Для сложных систем с большим числом элементов и их выходных параметров рассматривается столько структурных схем, сколько может быть сочетаний возможных отказов по всем параметрам.

Поскольку большинство элементов автомобиля (сложной системы) могут выходить из строя по разным параметрам, при оценке долговечности элемента следует это учитывать. Например, кузов легкового автомобиля может быть отправлен в утиль при серьезных повреждениях в дорожно-транспортных происшествиях (ДТП) и при сильной коррозии или усталостных разрушениях. Допустим, что средний ресурс кузова по ДТП 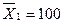тыс. км, а средний ресурс кузова по коррозии 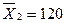тыс. км при среднем квадратическом отклонении 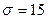тыс. км. Какой в этом случае средний ресурс кузова?

При решении подобной задачи следует представить структурную схему безотказности элемента по параметрам. В данном примере общая безотказность будет выражаться произведением безотказностей 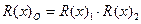. Наработка на отказ по ДТП является случайной величиной, распределенной по экспоненциальному закону 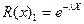, где .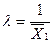

Наработка на отказ по коррозии является случайной величиной, распределенной по нормальному закону 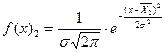и .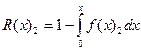

Подставляя выражения безотказностей по отдельным параметрам в формулу общей безотказности, получим 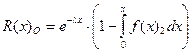. Отсюда можно найти средний ресурс кузова путем интегрирования кривой безотказности 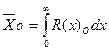. В результате решения, получена формула среднего ресурса кузова, который выбывает из эксплуатации или из-за ДТП, или вследствие коррозии и усталостных трещин 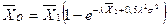. Для заданных в примере числовых характеристик 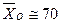тыс. км. Если за счет применения новых антикоррозийных покрытий повысить ресурс кузова в два раза, то общий средний ресурс станет равным 90,8 тыс. км.

Из проведенных расчетов можно сделать важные практические выводы:

1. Если деталь автомобиля (элемент сложной системы) имеет несколько выходных параметров, характеризующихся некоторыми средними ресурсами, то общий средний ресурс всегда будет меньше меньшего ресурса.

2. Для повышения среднего ресурса детали в первую очередь следует повышать ресурс по самому «слабому» параметру, который дает наименьшее значение среднего ресурса.

Вопросы для самоконтроля по третьему разделу

1. По каким признакам детали, агрегаты и системы автомобиля можно отнести к последовательно или параллельно включенным элементам сложной системы?

2. Нужно ли для повышения среднего ресурса автомобиля в два раза повышать средний ресурс всех деталей в два раза?

3. Как рассчитать безотказность сложной системы из последовательно включенных элементов при известных безотказностях?

4. Как рассчитать безотказность сложной системы из параллельно включенных элементов при известных безотказностях?

5. Почему резервирование как метод повышения надежности находит ограниченное применение в конструкции автомобилей?

6. Что нужно сделать для оценки безотказности сложной системы, если ее элементы имеют по нескольку выходных параметров?

7. Если ресурс объекта ограничивается действием разных процессов и известны средние ресурсы по каждому из них, то чему будет равен средний ресурс объекта?

Л9