Модели источников сообщений. Конечный вероятностный источник сообщений

Большинство информационных процессов связано не с отдельными сообщениями, а с последовательностями (потоками) сообщений. Например, при чтении человек анализирует последовательность букв, образующих слова и текст в целом; данные, поступающие от измерительных устройств или передающиеся по каналам связи, представляют собой последовательности сообщений. Для описания (моделирования) подобных ситуаций удобно ввести формальное понятие конечного (комбинаторного)источника сообщений.

Конечным (комбинаторным) источником называется произвольное множество 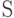. Элементы множества 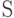обычно называются сообщениями. Источник может породить любое из этих сообщений.

В некоторых случаях бывает известно, что в последовательностях сообщений одни сообщения встречаются чаще, чем другие. Например, в текстах на русском языке буквы "о", "е" встречаются более чем в 10 раз чаще букв "щ", "э", "ф" [30]. В других естественных языках наблюдается аналогичная ситуация. Использование дополнительной информации о частотах появления сообщений вероятностного источника может повысить эффективность обработки данных.

Формализацией понятия частоты появления того или иного события в математике является его вероятность. Вероятность события 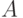обозначают обычно символом . Вероятность некоторого события (сообщения) можно представлять себе как долю тех случаев, в которых оно появляется, от общего числа появившихся событий (сообщений).

Так, если заданы четыре сообщения 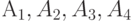с вероятностями 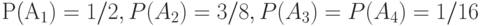, то это означает, что среди, например, 10000 переданных сообщений около 5000 раз появляется сообщение 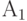, около 3750 - сообщение 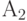и примерно по 625 раз - каждое из сообщени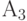й и .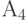

Распределение вероятностей появления отдельных сообщений в последовательности является важной ее характеристикой и существенно влияет на дальнейшие процессы обработки сообщений. Для дальнейшего удобно ввести формальное понятие конечного вероятностного источника сообщений.

Вероятностным источником 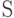назовем произвольное множество (сообщений) с вероятностями (частотами) появления каждого из них. Удобно представлять вероятностный источник в виде таблицы.

Вероятностный источник сообщений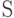

Сообщение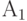
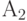
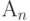
Вероятность появления сообщения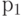

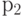
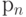
С позиций теории вероятностей вероятностный источник представляет собой дискретное распределение.

Характерной особенностью вероятностного источника является отсутствие полной определенности в поступлении очередного сообщения источника. Степень неопределенности для различных источников может значительно отличаться. Например, если рассматривать в качестве источника номера лотерейных билетов, крайне трудно определить номер оче-редного выигрышного билета. Однако если сообщениями источника считать исходы розыгрыша крупного выигрыша (автомобиля или квартиры) для конкретного билета, то сообщение такого источника предсказать не трудно. Скорее всего, на данный лотерейный билет крупного выигрыша не будет.

Для практики желательно уметь оценивать степень неопределенности различных вероятностных источников. Рассмотрим источник с равновероятными сообщениями. Понятно, что степень неопределенности такого источника зависит от . При 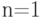неопределенность отсутствует, т. к. может появиться только одно единственное сообщение. При больших неопределенность больше (трудно предсказать появление какого-то определенного сообщения из возможных). Из рассмотренного примера следует, что функция, описывающая неопределенность источника, должна принимать нулевое значение в случае отсутствия неопределенности (при 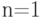), а при увеличении она должна возрастать. Можно показать [31], что, наложив ряд простых и естественных требований на функцию, которая должна характеризовать неопределенность вероятностного источника, можно определить вид такой функции.

Неопределенность вероятностного источника 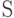с множеством сообщений 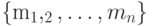, вероятности появления которых равны 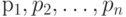соответственно, принято описывать функцией (величиной)

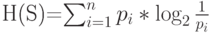
( 6.1)

Величина называется энтропией источника сообщений 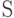. К. Шеннон предложил использовать энтропию для описания источников информации [30].

Неопределенность источника можно трактовать как его информативность. Действительно, если неопределенность источника мала или даже равна 0, то очередное сообщение не несет новой информации, т. к. легко может быть предсказано заранее. И наоборот, очередное сообщение неопределенного источника плохо предсказуемо, скорей всего оно будет новым, отличным от любого ожидаемого сообщения.

Входящее в выражение (6.1) для энтропии выражение 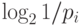можно рассматривать как информативность (неопределенность) 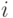-го сообщения источника, поскольку оно вполне соответствует интуитивному представлению о неопределенности. Энтропию можно рассматривать как среднюю информативность всего источника .

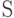От вероятностного источника зависит выбор оптимального в среднем способа кодирования сообщений.