Потенциальная энергия взаимодействия системы зарядов
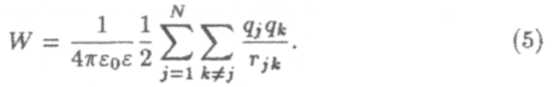
| как это было показано в (4). Один из способов написания суммы по парам таков: |
Ранее мы определили, что потенциальная энергия двух зарядов характеризует работу, совершаемую внешними силами по перемещению заряда q0 из бесконечности на расстояние r до заряда q.
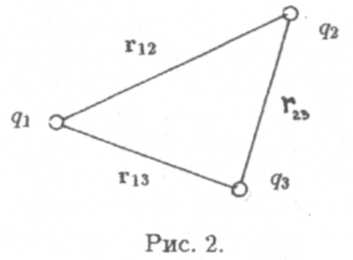
Если система состоит из трех зарядов, то ее полная потенциальная энергия будет равна работе внешних сил по перемещению всех трех зарядов из бесконечности в место их расположения (рис. 2).
Работа по сближению зарядов q2 и q1 определяется выражением:
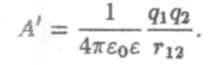
Чтобы перенести заряд q3 из бесконечности в точку, находящуюся на расстоянии r13от q1 и на расстоянии r23от q2, требуется совершить работу, равную благодаря суперпозиции электрических взаимодействий сумме двух работ: одна из которых необходима для переноса q3 в указанную точку, если имеется только один заряд q1, а другая требуется для переноса q3 в эту точку при наличии только одного заряда q2
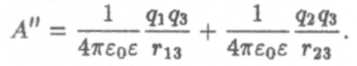
Следовательно, потенциальная энергия, определяемая полной работой, затраченной на образование указанного расположения трех зарядов (рис. 2), равна:
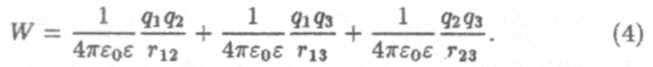
Этотрезультат можно обобщить на любое количество зарядов. Если мы имеем N различных зарядов, любым образом расположенных в пространстве, то электрическая потенциальная энергия системы вычисляется путем суммирования по всем парам,
Знак двойной суммы означает следующее: возьмите j = 1 и суммируйте по к = 2,3,4.. N; затем возьмите j = 2 и суммируйте по к = l,3,4…V, и т.д. до j = N. Ясно, что при этом каждая пара войдет в сумму дважды, поэтому перед знаком суммы стоит множитель 1/2.
Дата добавления: 2015-08-11; просмотров: 1257;
