Последовательное, параллельное и с обратной связью.

Абстрактный автомат (АА) задается шестеркой (шестикомпонентным вектором):

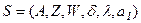
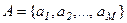- множество (алфавит) состояний;

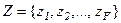- множество (алфавит) входных сигналов;

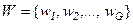- множество (алфавит) выходных сигналов;

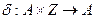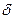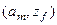- функция переходов автомата. Функция паре ставит в соответствие некоторое состояние :

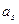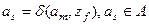
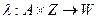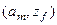функция выходов автомата. Функция паре ставит в соответствие некоторый выходной сигнал

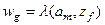
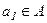- начальное состояние АА.

Автомат называется конечным, если конечны множества , , .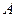

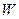В дальнейшем будем иметь ввиду только конечные автоматы.

Автомат называется детерминированным, если для всех пар 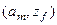функция 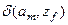имеет единственное значение. В дальнейшем будем иметь ввиду только детерминированные автоматы. Наряду с детерминированными существуют автоматы недетерминированные и стохастические.

В рамках курса будем рассматривать как синонимы следующие термины:

- алфавит, буква, символ;

- слово, цепочка.

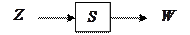Смысл вышеприведенных терминов очевиден и не требует формальных определение.

АА имеет один вход и один выход:

Автомат работает в дискретном времени, принимающем значения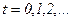

Всегда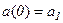

В момент времени 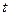автомат находится в состоянии 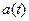. На его вход поступает входной символ 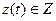. В качестве реакции на входной символ автомат выдает некоторую букву 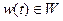выходного алфавита: 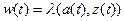. Затем в соответствии с функцией перехода 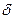переходит в следующее состояние: .

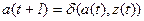На этом заканчивается один цикл работы автомата.

Последовательность символов входного алфавита: 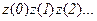задает входное слово (слово входного алфавита).

Последовательность символов выходного алфавита 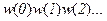задает выходное слово (слово выходного алфавита).

Работа АА состоит в преобразовании слов входного алфавита в слова выходного алфавита.

В АА отвлекаются от внутренней структуры автомата, рассматривая его как “черный ящик”. При этом основное внимание уделяется поведению автомата относительно внешней среды. В качестве элементов, связывающих автомат с внешней средой, выступают входные и выходные слова.

Введение состояний в описание устройства позволяет запоминать и учитывать предысторию поведения автомата. Это дает возможность строить устройства, которые на одни и те же входные сигналы в разные моменты времени реагируют по-разному.

Поведение комбинационных схем описывается системой булевских функций, в которых аргументам соответствуют только входные сигналы. КС всегда на данный набор входных сигналов вырабатывает определенный набор выходных сигналов, не зависящий от времени. КС можно рассматривать как частный случай автомата с одним состоянием:

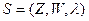
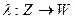
Основными видами соединений 2х автоматов являются:

- параллельное;

- последовательное;