Статический момент фигуры

В теории геометрических характеристик сечений бруса исследуемым объектом является площадь этого сечения. Рассмотрим сначала бесконечно малую площадь dA. Расстояние а от центра dA до оси х назовем ее плечом.

Рис1.1

Статическим моментом dS_x относительно оси х бесконечно малой площади dA называется произведение dA на а:

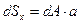
(1.1)

Учитывая, что а=у запишем:

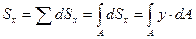Если фигура имеет конечную площадь, то мы её можем разбить на бесконечно малые площади и для каждой из них найти статический момент. Просуммировав их, найдем статический момент всей фигуры относительно оси х.

(1.2)

Аналогично вводится понятие статического момента относительно оси у

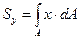(1.3)

Вычисление статических моментов.

Используем для получения формулы вычисления S_x , S_у аналогию с моментом силы в теоретической механике. Будем считать что наша фигура dA имеет толщину t, тогда объём фигуры :

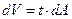
Вес dР фигуры dA равен произведению удельного веса 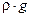на объёмdV :

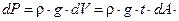
Обозначаем ,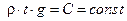

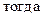
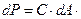
Вес Р всей фигуры вычисляется аналогично:

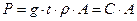(1.4)

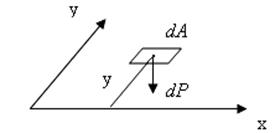
Рис.1.2

Момент силы dР относительно оси х будет:

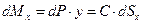(1.5)

Суммируя эти моменты, получим :

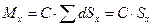(1.6)

Из теоретической механики известно, что равнодействующий момент можно вычислить через равнодействующую силу Р следующимобразом:

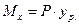
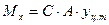где 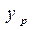- координата точки приложения силы Р. Но равнодействующая силы тяжести фигуры приложена в центре тяжести, значит:

(1.7)

Подставляя слева (1.4) получим:

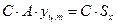
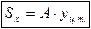Таким образом:

(1.8)

Аналогично вычисляется статический момент относительно оси у:

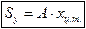
(1.9)

Отсюда вытекают формулы для вычисления координат центра тяжести фигуры: 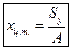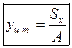(1.10)