Осевой момент инерции

Рассмотрим бесконечно малую площадь dA (см. рис.1.3).

Осевым моментом инерции dJ_x относительно оси х бесконечно малой площади dA называется произведение dA на квадрат плеча, то есть на у²:

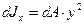
Рис. 1.3

Если фигура имеет конечную площадь А, то как обычно, разбиваем ее на бесконечно малые площади и для каждой из них вычисляем dJ_x. Просуммировав их, найдем осевой момент инерции всей фигуры:

(1.11)

Аналогично вводится осевой момент инерции относительно оси у:

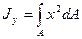(1.12)

Из (1.11), (1.12) видно, что осевые моменты инерции 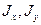никогда не равны нулю и не бывают меньше нуля, они всегда положительны.