Течение газа в соплах
Сопло является трансформатором энергии в ракетном двигателе и его назначение - получение наибольшего значения скорости истечения рабочего тела, существенно превышающего значение скорости звука. Это возможно при использовании сопла особой конфигурации, отличной от насадки схемы рис 5.2.
Рассмотрим адиабатическое течение газа в канале переменного сечения. Независимыми переменными в данной системе пусть будут ρ и S. Уравнение состояния имеет вид: 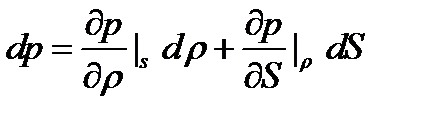 (а)
(а)
для изоэнтропического течения 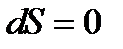 и
и 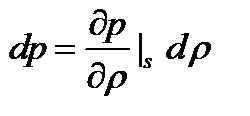 (б) Скорость распространения звука в газах
(б) Скорость распространения звука в газах 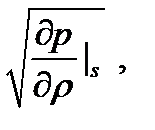 тогда
тогда  . С учетом (а) и (б) получим:
. С учетом (а) и (б) получим:
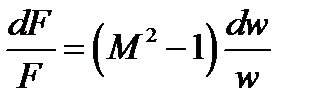 ,
,
где 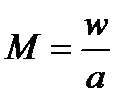 – число Маха, отношение местной скорости газа к местной скорости звука в нем, мера сжимаемости газа.
– число Маха, отношение местной скорости газа к местной скорости звука в нем, мера сжимаемости газа.
Пусть движение газа происходит с возрастанием скорости и М<1 (дозвуковое течение). Тогда 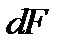 и
и 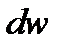 имеют разные знаки, разгон потока происходит при уменьшении площади канала по осевой координате. При сверхзвуковом течении (
имеют разные знаки, разгон потока происходит при уменьшении площади канала по осевой координате. При сверхзвуковом течении ( 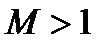 ) увеличение скорости происходит при
) увеличение скорости происходит при 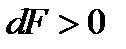 , т.е. канал должен расширяться. Физически это означает, что плотность газа упала настолько, что постоянный расход газа сохраняется при одновременном увеличении скорости потока и площади канала.
, т.е. канал должен расширяться. Физически это означает, что плотность газа упала настолько, что постоянный расход газа сохраняется при одновременном увеличении скорости потока и площади канала.
Для достижения сверхзвуковой скорости изменение площади канала по осевой координате должно меняться следующим образом. При выходе из ресивера сечение канала должно уменьшаться до места достижения скорости звука ( 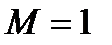 ), здесь канал имеет минимальное сечение (
), здесь канал имеет минимальное сечение ( 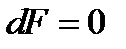 ), дальнейшее увеличение скорости газа при
), дальнейшее увеличение скорости газа при 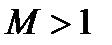 возможно только при увеличении площади поперечного сечения канала. Сопло для получения сверхзвуковой скорости с таким изменением площади поперечного сечения вдоль оси предложил шведский инженер Лаваль в 1908 году. Из (5.3) следует, что скорость истечения не зависит от значения давления в ресивере и от разности давлений в ресивере и окружающей среде, а определяется температурой и отношением давлений в ресивере и на срезе сопла. Но даже при истечении в вакуум
возможно только при увеличении площади поперечного сечения канала. Сопло для получения сверхзвуковой скорости с таким изменением площади поперечного сечения вдоль оси предложил шведский инженер Лаваль в 1908 году. Из (5.3) следует, что скорость истечения не зависит от значения давления в ресивере и от разности давлений в ресивере и окружающей среде, а определяется температурой и отношением давлений в ресивере и на срезе сопла. Но даже при истечении в вакуум 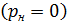 скорость истечения имеет конечное значение
скорость истечения имеет конечное значение
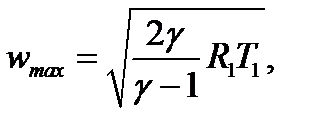
являющееся теоретическим пределом.
При достижении потоком скорости звука наступает кризис течения, это происходит в минимальном сечении сопла и параметры газа в нем имеют критические значения – 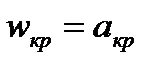 . Скорость звука переменна по длине сопла.
. Скорость звука переменна по длине сопла.
Умножим (5.3) на 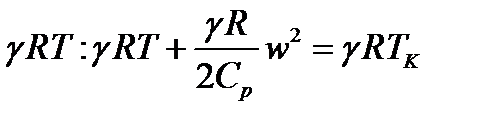 , с учетом уравнения Майера получим:
, с учетом уравнения Майера получим:
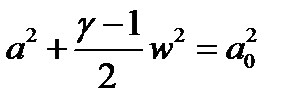 , (6.1)
, (6.1)
т.е. при адиабатическом течении сумма 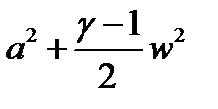 постоянна и равна скорости звука в заторможенном газе, величина
постоянна и равна скорости звука в заторможенном газе, величина 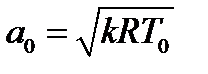 есть характеристика торможения.
есть характеристика торможения.
В минимальном сечении 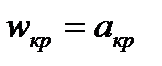 , из (6.1) получим:
, из (6.1) получим:
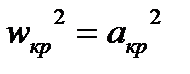
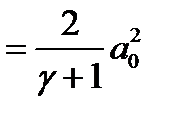 ,
,
тогда температура газа в минимальном сечении сопла
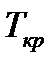
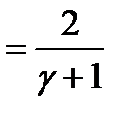
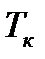 .
.
В адиабатическом процессе 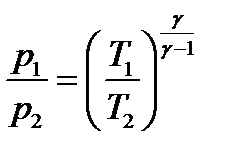 , отсюда давление в минимальном сечении
, отсюда давление в минимальном сечении
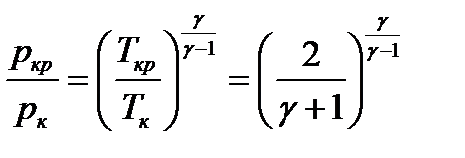 .
.
В практических расчетах параметров изоэнтропического одномерного течения газа в соплах используют газодинамические функции - безразмерные функции некоторых аргументов, определяемые отношениями параметров в i-м сечении сопла к значениям этих же параметров для заторможенного газа в этом же сечении сопла.
В качестве аргумента используют приведенную скорость 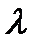 – отношение скорости газа в i-м сечении сопла к критической скорости
– отношение скорости газа в i-м сечении сопла к критической скорости
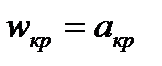 ,
,
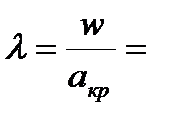
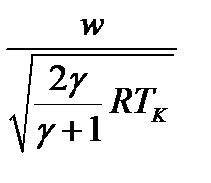 .
.
Значение 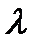 изменяется от
изменяется от 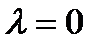 в ресивере (корпусе двигателя, камере сгорания) до предельного при истечении в вакуум
в ресивере (корпусе двигателя, камере сгорания) до предельного при истечении в вакуум 
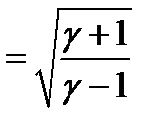 .
.
Связь между приведенной скоростью и числом Маха:
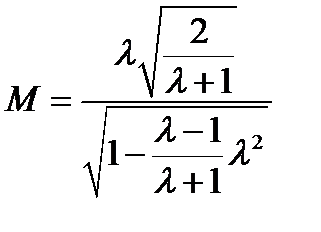 ,
, 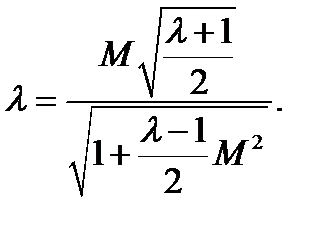
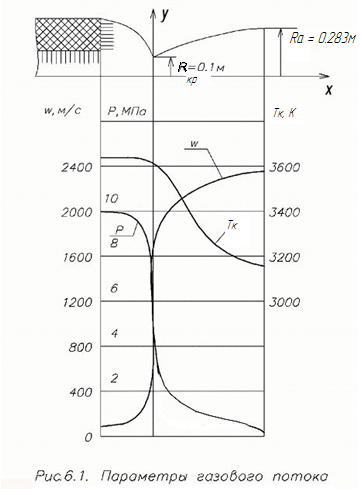
В практике расчетов используют таблицы, в которых приведены значения функций, что позволяет вычислить параметры потока в любом сечении сопла при известных параметрах заторможенного газа и относительном диаметре канала (сопла). В качестве примера на рис.6.1 показано распределение параметров газового потока по тракту двигателя, рассчитанного с помощью газодинамических функций.
На практике, при проектировании ракетных двигателей условно считают, что критическое и минимальное сечение сопла совпадают.
Исследование течений в соплах для профилирования их и расчетов параметров тепломассообмена проводят на основе модели невязкого и нетеплопроводного газа. Движение такого газа описывают уравнения Эйлера и для случая осесимметричного стационарного течения при отсутствии массовых сил они имеют вид:
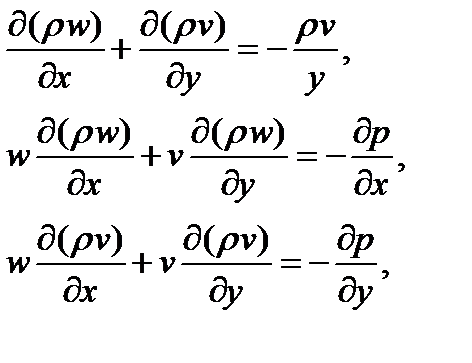
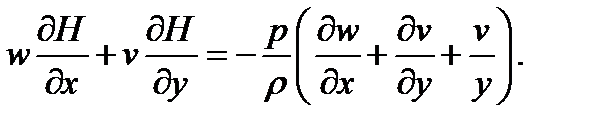 (6.2)
(6.2)
Здесь добавлены уравнения неразрывности и сохранения энтальпии H движущегося газа, ось 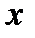 направлена по оси симметрии двигателя (рис. 6.1). В механике жидкости и газа существует направление - вычисление параметров двухфазных (продукты сгорания металлизированных топлив) течений в соплах РД.
направлена по оси симметрии двигателя (рис. 6.1). В механике жидкости и газа существует направление - вычисление параметров двухфазных (продукты сгорания металлизированных топлив) течений в соплах РД.
Уравнения (6.2) есть система квазилинейных (линейных относительно производных) уравнений. В зависимости от скорости потока система может быть эллиптического типа ( 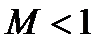 ), параболического (
), параболического ( 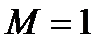 ) или гипербо-лического типа (
) или гипербо-лического типа ( 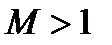 ).
).
6.2. Профилирование камеры жидкостного ракетного двигателя
6.2.1. Определение размеров камеры сгорания
Одним из факторов, определяющим полноту сгорания топлива и тем самым влияющим на совершенство камеры сгорания, является время, которое может быть отведено для протекания химических реакций горения. Оно определяется скоростью газа в камере сгорания, используемым для процессов горения объемом камеры сгорания Vк , а также давлением и температурой.
В настоящее время нет способа расчета объема камеры сгорания, учитывающего действительно происходящие в ней физико-химические процессы, поэтому объем камеры сгорания, необходимый для полного сгорания топлива, определяют с использованием экспериментальных данных.
На рис. 6.2 показан график изменения удельного объема продуктов сгорания по времени от начального удельного объема жидкого топлива 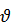 T до удельного объема продуктов сгорания
T до удельного объема продуктов сгорания 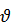 к по окончании процесса горения.
к по окончании процесса горения.
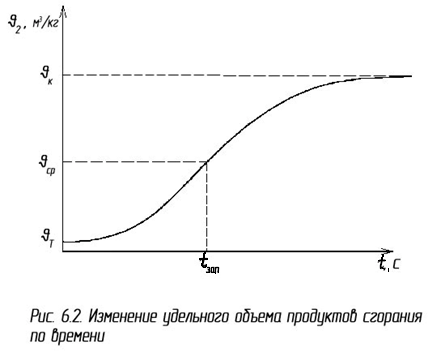
Предположим, что до некоторого времени запаздывания tзап реакции горения не происходят, а во время tзап процесс горения протекает мгновенно. При этом, исходя из графика, средний удельный объем продуктов сгорания 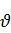 ср в момент времени tзап будет равен
ср в момент времени tзап будет равен 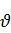 ср=0.5
ср=0.5 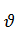 к. Средний удельный объем позволяет найти истинное время пребывания топлива и его продуктов сгорания в камере сгорания:
к. Средний удельный объем позволяет найти истинное время пребывания топлива и его продуктов сгорания в камере сгорания:
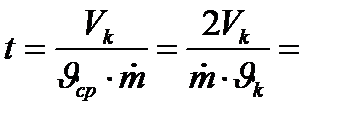
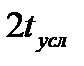 , (6.3)
, (6.3)
где  – условное время пребывания.
– условное время пребывания.
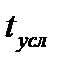
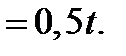 (6.4)
(6.4)
Отсюда можно получить
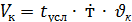 . (6.5)
. (6.5)
Обработка экспериментальных данных для различных топлив (двигателей) показала, что
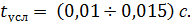
Определив из термодинамического расчета 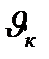
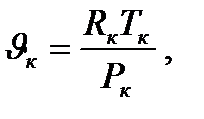 (6.7)
(6.7)
можно рассчитать объем камеры сгорания 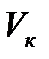 .
.
С другой стороны
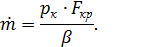
Тогда из (6.5) следует
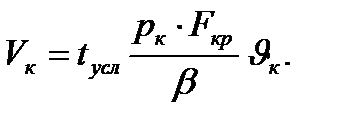 (6.8)
(6.8)
Преобразуем (6.8)
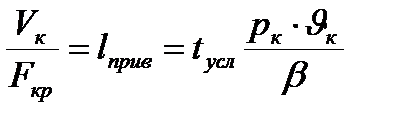 , (6.9)
, (6.9)
где 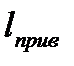 - приведенная длина камеры сгорания.
- приведенная длина камеры сгорания.
Тогда для объема камеры сгорания получим выражение
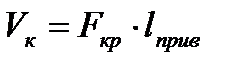 . (6.10)
. (6.10)
Обработка экспериментальных данных для различных топлив (двигателей) показала, что:
- для топлив HN03 + НДМГ, N204 + НДМГ, 02ж + керосин – lприв = (1,0÷1,5)м;
- для топлива О2ж + Н2ж - lприв = (0,5 ÷1,0) м.
Определим размеры камеры сгорания. Для цилиндрической камеры сгорания
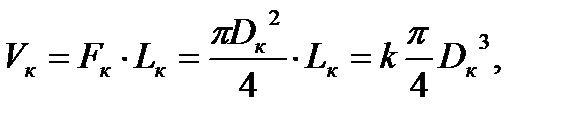 (6.11)
(6.11)
где 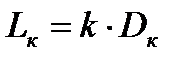
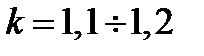

Тогда,
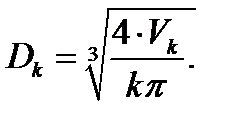 (6.12)
(6.12)
Дата добавления: 2015-08-11; просмотров: 3167;
