Термогазодинамика потока рабочего тела

Перейдем к термогазодинамике потоков – определению параметров движущегося рабочего тела. Рассмотрим наиболее простую модель движения газа: одномерное установившееся адиабатическое (изоэнтропическое) течение идеального газа, когда в каждой точке потока параметры не изменяются во времени и зависят только от осевой координаты x движения. Целью расчетов является определение средних по площади F поперечного сечения канала с осевой координатой x значений скорости w, давления p, плотности 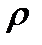и температуры T.

Значения искомых параметров находят из решения уравнений неразрывности, I закона термодинамики, состояния и движения газа. Уравнение неразрывности получают из формулировки закона сохранения вещества в гидродинамике:

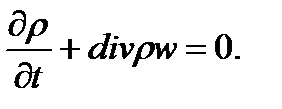
В рассматриваемом случае одномерного движения уравнение неразрывности принимает вид

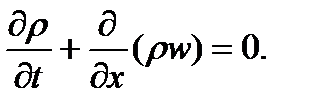
Для одномерного стационарного течения газа имеем: 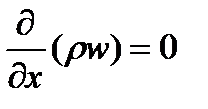, т.е.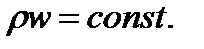

Тогда расход газа через поперечные сечения канала Дифференциальная форма уравнения неразрывности:

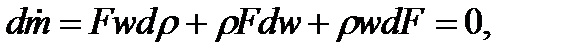разделим на и получим

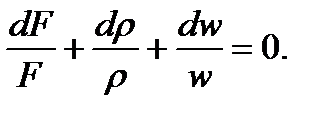
Движение газа в одномерном поле давления p=f(x) с градиентом dp/dx приводит к действию на элементарный объем Fdx силы (dp/dx) Fdx,сообщающей массе газа 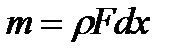в стационарном потоке ускорение

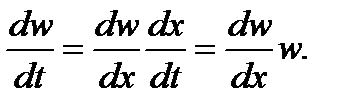
В соответствии со II законом Ньютона уравнение движения примет вид

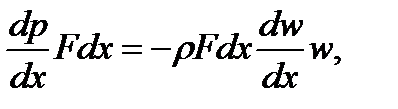
или

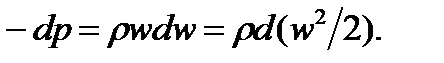
Откуда при 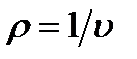получим:

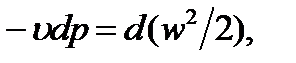
где 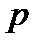и 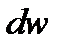имеют разные знаки – скорость возрастает в направлении уменьшения давления.

Из I закона термодинамики следует, что теплота 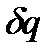, подведенная к элементарной массе газа, тратится на увеличение его энтальпии и кинетической энергии 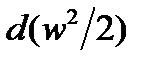, которую и превращают в механическую энергию различные энергетические установки

Если нет теплообмена с окружающей средой ( 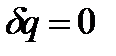), то 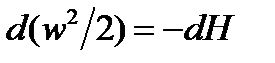, после интегрирования получим

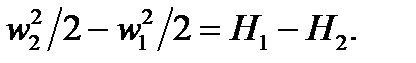(5.1)

Рассмотрим адиабатическое истечение газа из конического насадка схемы рис. 5.2.

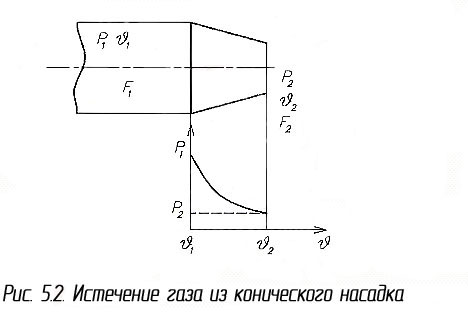
Скорость потока вычисляют из (5.1) при допущении, что в ресивере w₁=0 – в любом сечении сопла 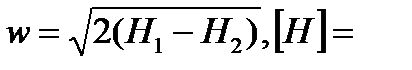Дж/кг, 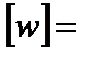м/с.

Для адиабатического процесса 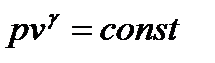и располагаемая работа

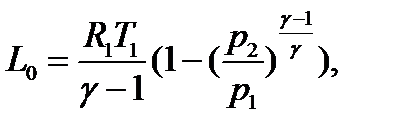(5.2)
в то же время 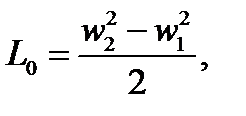тогда из (5.2)

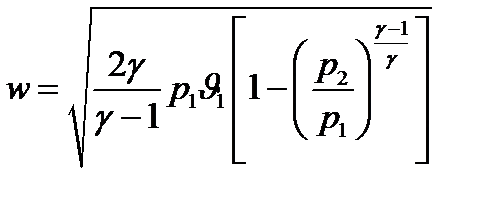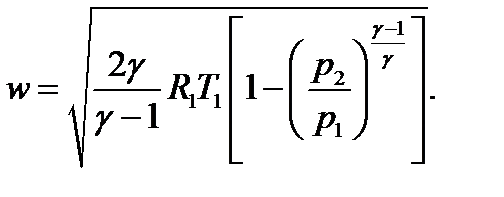или (5.3)

Расход газа с учетом уравнения адиабаты, неразрывности и (5.3):

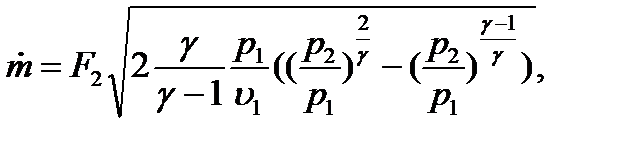(5.4)
т.е. при заданных F₂ и параметрах ресивера расход определяется значением p₂.

Рассмотрим теперь параметры заторможенного потока. В адиабатическом процессе 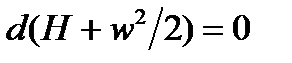или 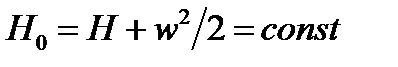. Энтальпией торможения называют величину H₀ – ее имеет газ до начала истечения из ресивера или при полной остановке движения без отвода теплоты и потерь энергии.

Есть и другая постоянная - сумма, вытекающая из определения энтальпии:

(5.5)

и (5.6)

Сумма термодинамической температуры T и динамического повышения температуры 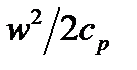при торможении потока есть температура торможения T₀.

Из уравнения Бернулли для несжимаемой жидкости можно получить выражение для давления торможения

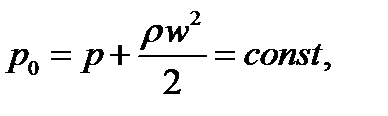
где p – статическое термодинамическое давление (давление движущегося газа),

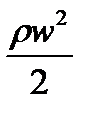- динамическое давление (скоростной напор).

Для сжимаемого газа уравнение Бернулли принимает вид (с учетом: 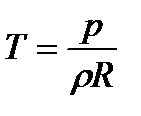и уравнения Майера ):

.

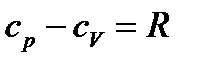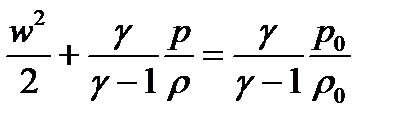ЛЕКЦИЯ 6