На орбиту без учета сопротивления атмосферы .

Орбита , на которую выводится ИСЗ с течением времени изменяется , это связано с тем , что на спутник действуют :

§ хотя и небольшие , но в течении длительного времени аэродинамические силы ;

§ переменное с течением времени гравитационное поле , обусловленное влиянием других небесных тел (кроме Земли) и в первую очередь Луны .

Эти обстоятельства необходимо учитывать при определении :

§ времени существования спутника на орбите ;

§ географического положения спутника по отношению к поверхности Земли в каждый момент времени ;

§ и т.д.

Задача точного расчета движения спутника является кропотливой и сложной . Если необходимо исследовать движение спутника на небольшом интервале времени (после запуска) , то действительное движение можно заменить на более простое , сводя задачу к движению двух тел .

Задача будет более простой , если исходить из Кеплерового центрального поля тяготения и не учитывать сплюснутость Земли и ее суточные вращения . Траектория полета ИСЗ при этих допущениях представляет собой эллипс , в одном из фокусов которого находится центр Земного шара .

Частным случаем эллиптической траектории спутника является окружность с центром в центре Земного шара .

При выводе ИСЗ на ту или иную орбиту главный интерес представляют такие законы управления полетом ракеты-носителя , которые обеспечивают наименьшие энергетические затраты .

Пример : наименьший расход топлива необходимый для вывода ИСЗ на заданную орбиту .

Решение получается достаточно просто , если не принимать во внимание аэродинамические силы , действующие РН во время ее полета в плотных слоях атмосферы . Для спутника запущенного с поверхности Земли , такое решение будет иметь приближенный характер , а для спутника с Луны такое решение будет очень близко к действительному . Однако и для спутника с Земли такая постановка имеет смысл , т.к. позволяет сделать некоторые общие заключения .

Пренебрегая аэродинамическими силами будем считать , что на РН действует только сила тяги двигателей и сила тяжести Земли .

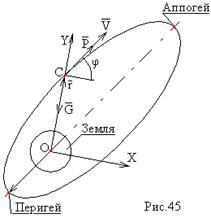В момент вывода ИСЗ на орбиту , кривизной Земли и ее суточным вращением пренебрегаем , а ускорение силы тяжести считаем постоянным для всех высот полета .

Задача заключается в отыскании такого закона и изменения силы тяги функции времени (по величине и направлению) , чтобы на заданной конечной высоте полета ( Н_к ) вертикальная составляющая скорости ИСЗ ( V_ку ) , была равна нулю , а горизонтальная – ( V_кх ) имела максимальное значение .

Запишем уравнение движения ИСЗ в проекциях на оси координат OXY :

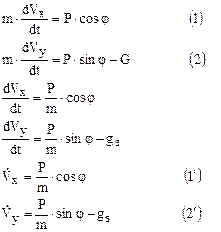
φ – угол между осью ОХ (земной системы координат) и осью двигателя (если двигатель соединен неподвижно с ракетой , то φ тождественен углу тангажа Θ ) .