Гидравлическая характеристика горизонтальных обогреваемых труб

Для упрощения задачи возьмем горизонтальную трубу без местных сопротивлений ( Δp_М = 0), будем считать, что сопротивление ускорения мало, Δp_уск = 0. Тогда полное гидравлическое сопротивление будет равно сопротивлению трения, Δp = Δp_ТР.

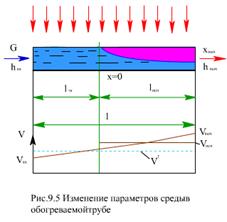
Горизонтальная труба (рис.9.5) длиной l, м, и с внутренним диаметром d, м, равномерно обогреваются, тепловой поток на 1 м длины трубы q_l, кВт/м. На вход трубы подается вода, недогретая до кипения (h_ВХ < h'). На экономайзерном участке вода нагревается до энтальпии кипения и затем начинает испаряться; на выходе из трубы - пароводяная смесь с x_ВЫХ.

Длина экономайзерного участка определится из уравнения теплового баланса

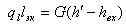
(9.28)

(9.29)

Длина экономайзерного участка при G и q₁ = const зависит от недогрева воды на входе до кипения Δh_нед=h' - h_ВХ.

Длина испарительного участка l_ИСП = l - l _ЭК, или по тепловому балансу

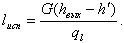
(9.30)

Учитывая разное фазовое состояние на участках, сопротивление трения в трубе представим как сумму сопротивлений на экономайзерном Δр_ЭК и испарительном Δр_ИСП участках

Δр = Δр_ТР = Δр_ЭК + Δр_ИСП

Сопротивление на экономайзерном участке при длине l_ЭК по (9.29)

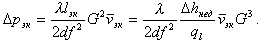
(9.31)

Получилась кубическая зависимость, так как l_ЭКзависит от расхода G.

При небольшом недогреве Δh_нед можно принять без предварительного расчета.

Сопротивление на испарительном участке

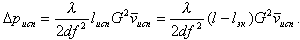
(9.33)

На испарительном участке удельный объем изменяется существенно, и, в общем виде, есть среднеинтегральная величина. Возьмем первое, линейное, приближение

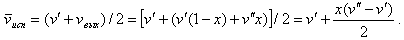
(9.34)

В выходном сечении массовое паросодержание

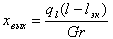
(9.35)

Подставляя в (9.34) выражения для х_ВЫХ (9.35) и затем для l_ЭК (9.29), получаем

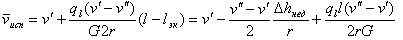
(9.36)

Введем обозначение

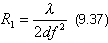
(9.37)

Подставляем в (9.31) зависимости (9.32) и (9.33) с учетом (9.29), (9.36) и проводим перегруппировку членов формулы. В результате получаем

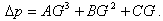
(9.38)

где

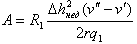
(9.39)

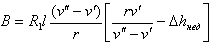
(9.40)

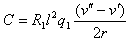
(9.41)

Таким образом, гидравлическая характеристика обогреваемой горизонтальной трубы при движении двухфазного потока с недогревом выражается уравнением третьей степени (9.38).

Решение уравнения третьей степени может иметь один действительный и два мнимых корня (кривая 7, рис.9.6) или все три действительных корня (кривая 2, рис.9.6). В первом случае имеем однозначную характеристику; во втором случае кривая имеет точку перегиба и два экстремума, а перепаду давления Δp₀ отвечают три расхода среды: G₁, G₂ и G₃ Такая характеристика называется многозначной. Проведя горизонтали через точку минимума и максимума кривой 2, получим диапазон неоднозначности по расходу (G_МИН…G_МАКС) и сопротивлению (Δp_МИН…Δp_МАКС). Вне этого диапазона кривые однозначны.

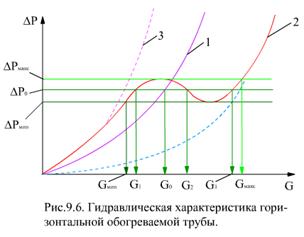
При малых расходах (G < G _МИН) длины экономайзерного и испарительного участков уменьшаются и может появиться перегревательный участок, причем с уменьшением G доля его возрастет, кривая 2 при этом приближается к гидравлической характеристике при прохождении через трубу перегретого пара (кривая 3, рис.9.6). При больших расходах среды (G > G _МАКС), наоборот, длины экономайзерного и испарительного участков растут, затем испарительный участок исчезает, и сопротивление определяется однофазным потоком недогретой до кипения жидкости (кривая 4). В области неоднозначности расхода (С _МИН - G _МАКС) длина экономайзерного участка увеличивается, а испарительного - уменьшается, снижается также массовое паросодержание х за счет уменьшения парообразования (l_ИСП и G _П уменьшаются) и увеличения расхода жидкой фазы.

Нестабильность гидравлической характеристики опасна тем, что в параллельных трубах, находящихся практически в одинаковых условиях, расход среды может быть различным (G ₁ и G ₃, рис.9.6), паросодержание в них будет значительно различаться и возможно возникновение кризиса теплообмена. Кроме того, расходы через трубы могут изменяться самопроизвольно (G₁ или G₃), возникает пульсация потока во всем элементе, колебания температуры стенки. Все это может закончиться повреждением труб. Такие режимы недопустимы.

Выявим область неоднозначности. Для этого возьмем производную кубического уравнения по расходу dΔp/dG и определим точки экстремума

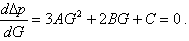
(9.42)

Точки экстремума

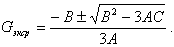
(9.43)

Зная комплексы А, В и С, определяем точки G'_ЭКСТР, а по ним значения Δp _МИН и Δp _МАКС

Формулу (9.43) можно использовать для нахождения параметров, при которых характеристика будет однозначной. Для этого необходимо, чтобы точки экстремума отсутствовали в положительной области G: были мнимыми или отрицательными.

В первом случае должно выполняться условие

Второе условие (G _ЭКСР < 0) возможно выполнить при В > 0 (в зависимости от D h _нед комплекс В может быть как положительным, так и отрицательным).

Из этих двух условий вытекает одно условие

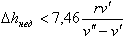
(9.45)

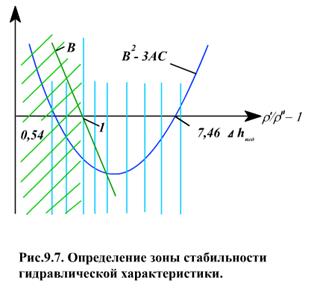
при котором гидравлическая характеристика горизонтальной трубы будет однозначна (рис 9.7).

При р = 11 МПа недогрев должен быть меньше 961 кДж/кг (h' = 1451 кДж/кг), при p = 16 МПа Δh_нед < 1558 кДж/кг (h' = 1651 кДж/кг). Этот параметр при высоком давлении не ограничивает выбор температуры на входе в горизонтальную одиночную трубу. При Δh_нед = 0 коэффициент А = 0, В = R₁lv'. С не зависит от недогрева, уравнение будет иметь вид

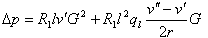
(9.46)

Пример. Оценим вклад слагаемых уравнения (9.46). Давление р = 16 МПа, v' = 0,00171 м³/кг, v" = 0,00933 м³/кг, r = 931,2 кДж/кг, примем l = 10 м, d = 20 мм, q_l = 500 кВт/м², пересчет q_l = 500 πdl/l = 500 πd = 500π·0,020 =31,4 кВт/м. Формулу (9.46) запишем в виде

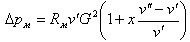
(9.47)

При ρw = 1000 кг/(м²·c) G = 0,314 кг/с , тогда

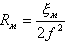
(9.48)

При G = 1 кг/с Δp/R₁·l = 1,71·10^-3+1,29·10^-33·10^-3

Расчет показывет, что вклад второго слагаемого в уравнении (9.46) с ростом G уменьшается и сопротивление трубы становится пропорционально квадрату расхода среды; коэффициент пропорциональности зависит от удельного объема воды v', длины трубы l и коэффициента гидравлического сопротивления R₁ (кривая 1, рис.9.8).

При Δh _нед > 0 коэффициент А > 0, В уменьшается и график зависимости Δр = f(G) изменяет форму (кривая 2); при Δh_нед > 7,46 rv'/(v"- v') график становится многозначным (кривая 3).