Уравнение движения двухфазного потока в трубах.
Для описания течения двухфазного потока (пароводяной смеси) используются две модели.
В модели гомогенного потока принимается, что обе фазы (жидкая и паровая) распределены равномерно и непрерывно одна в другой, при этом скорости их движения и температуры одинаковы. Другими словами, в гомогенном представлении движение двухфазного потока рассматривается как течение однородной сплошной среды. Полученные при этом параметры и характеристики потока называются расходными.
Вторая модель рассматривает двухфазный (гетерогенный) поток как систему из двух фаз, разделенных межфазными границами, движущихся с разными скоростями. Уравнения записываются отдельно для жидкой и паровой фазы. Начальные и граничные условия также записываются отдельно для фаз, при этом учитывается, что на границах раздела фаз имеют место механическое взаимодействие, массообмен и переток теплоты.
Параметры, характеризующие движение каждой из фаз в отдельности или поток в целом (с учетом движения отдельных фаз), называются истинными параметрами.
В инженерных расчетах за основу расчета двухфазных потоков принимается модель гомогенного потока, по которой определяются расходные параметры, а по ним рассчитываются истинные параметры с привлечением экспериментальных данных, устанавливающих зависимости между расходными и истинными параметрами двухфазного потока.
Соотношения между расходными и истинными параметрами двухфазного потока имеют сложный характер и зависят от структуры потока и распределения скоростей фаз.
Структура двухфазного потока показывает объемное содержание паровой и жидкой фазы, их границы, распределение по сечению трубы. По мере нагрева (охлаждения) потока массовые и объемные доли фаз изменяются, что сказывается на структуре потока и скоростях фаз. Предельными случаями являются однофазные потоки жидкости (масса пара равна нулю) и пара (жидкость отсутствует). Между этими крайними случаями можно выделить ряд устойчивых сочетаний структуры потока и скорости фаз, характеризуемых режимами течения двухфазных потоков. Каждому режиму течения можно соотнести свои зависимости между расходными и истинными параметрами двухфазного потока.
Рассмотрим участок обогреваемой трубы длиной l (рис. 8.5). Плотность теплового потока q1, кВт/м, постоянна по длине трубы. На вход в трубу подается вода с расходом G0, кг/с, и энтальпией h0, кДж/кг.
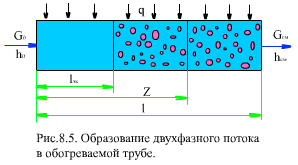
На экономайзерном участке lЭК происходит нагрев воды до температуры кипения ts (энтальпия воды на линии насыщения h). Давление потока р на рассматриваемом участке считаем постоянным (перепад давления мал). В гомогенном потоке фазы находятся в термодинамическом равновесии. При энтальпии потока h > h' начнется образование паровой фазы. Массовый расход паровой фазы обозначим D, кг/с, а расход жидкой фазы (воды) GВ, кг/с. В сечении z суммарный расход паровой и жидкой фаз G равен
G = D + GВ.
По уравнению неразрывности (условие сплошности)
G = G0 = const.
Суммарно количество теплоты, переносимое двухфазным потоком через сечение z
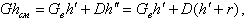
| (8.30) |
где h"- энтальпия пара на линии насыщения, кДж/кг; r - скрытая теплота парообразования, кДж/кг; hСМ- энтальпия пароводяной смеси.
Отсюда
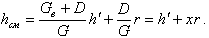
| (8.31) |
Величина x представляет собой расходное массовое паросодержание и характеризует долю пара в массовом расходе смеси
| x = D / G. | (8.32) |
Тогда расходное массовое содержание жидкости будет равно
| 1 - x = GВ / G. | (8.33) |
Для равновесного двухфазного потока
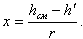
| (8.34) |
Величину x называют относительной энтальпией потока. Для жидкости, недогретой до ts получается x < 0; для жидкости на линии насыщения x = 0, для пара на линии насыщения x = 1; для перегретого пара x > 1.
По уравнению энергии (8.21) в сечении z
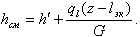
| (8.35) |
При этом величина
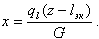
| (8.36) |
Длину экономайзерного участка lЭК можно определить, записав для него уравнение энергии (в виде теплового баланса)
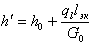
| (8.37) |
Отсюда
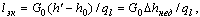
| (8.38) |
где Δhнед = h' - h0 - недогрев воды на входе в трубу до энтальпии кипения.
Подставляем lЭК в выражение для x (8.36)
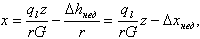
| (8.39) |
или
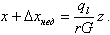
Полученные формулы дают возможность в любом сечении трубы определить массовое паросодержание , массовый расход пара (xG0) и воды (1 - x)G0.
По массовым расходам пара и воды можно определить расходные скоростные характеристики двухфазного потока:
приведенные скорости жидкой и паровой фаз - скорости, которые имели бы жидкость и пар, если бы только жидкость или только пар занимали все сечение f трубы
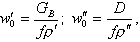
| (8.40) |
где ρ', ρ" - плотность воды и пара на линии насыщения, кг/м3;
скорость циркуляции - скорость, которую имел бы поток, если бы его плотность была равна плотности воды на линии насыщения:
| w0 = G / fρ'; | (8.41) |
скорость воды на входе в трубу
| wВХ = G / fρВХ, | (8.42) |
где ρВХ- плотность воды на входе в трубу;
скорость пароводяной смеси
| wСМ = G / fρСМ, | (8.43) |
где ρСМ - плотность пароводяной смеси.
С учетом введенных понятий о скоростях уравнение неразрывности можно записать в виде
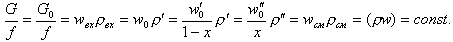
| (8.44) |
Из этого равенства можно определить искомую скорость через любую известную.
По длине трубы приведенные скорости воды и пара изменяются. Какое между ними соотношение? В сечении z массовый расход смеси G = D + GВ представим через скорости w0, w'0 и w"0
w0r'f = w''0r''f + w'0r'f.
Отсюда
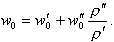
| (8.45) |
Получается, что хотя w'0 и w''0 изменяются по длине канала (w'0 уменьшается, a w''0 - растет), но сумма w'0 и w''0ρ'' / ρ' постоянна и равна скорости циркуляции.
По массовым расходам жидкости GВ и пара D можно рассчитать объемные расходы жидкости VВ и пара VП , м3/c:
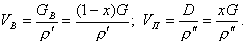
| (8.46) |
В гомогенном потоке скорости фаз равны, поэтому объемный расход Vсм = Gсм/ρсм.
Дата добавления: 2015-07-10; просмотров: 1583;
