Перепад давления при движении рабочей среды в трубе.

В результате решения уравнения движения получено в общем виде выражение (8.14) для перепада давления Δр при движении потока в трубе длиной l

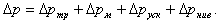
При движении однофазного потока для расчета сопротивления трения Δp_ТР, местного сопротивления Δp_М ,сопротивление ускорения Δp_УСК, и нивелирного сопротивления Δp_НИВ, применяются формулы (8.14 а) - (8.14 г) с учетом характеристик однофазного потока.

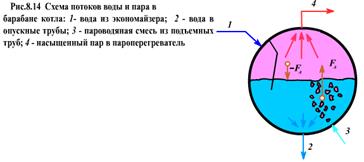
При движении двухфазного потока для расчета Δp используются те же формулы (8.14). Скорости потока w₁ , w₂, w_СР , плотность потока ρ_СР, а также в начале ρ₁ и конце ρ₂ участка определяются по истинным характеристикам двухфазного потока.

Учитывая, что истинные характеристики потока рассчитываются сложным образом по эмпирическим зависимостям, при расчете гидравлического сопротивления трения и местного сопротивления за основу берется гомогенная модель потока, а негомогенность действительного потока учитывается экспериментальными коэффициентами.

В формуле (8.14 а) по уравнению неразрывности заменим массовую скорость (φpw) через скорость циркуляции w₀ и плотность ρ' (ρw = ρ'w₀), среднюю скорость смеси w_СР выразим из соотношения ρw_ср = ρ'w₀. В результате получим

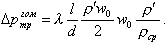
(8.53)

С учетом

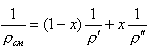
выразим

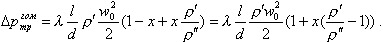
(8.54)

Еще раз отметим, что полученная формула справедлива для адиабатного (без обогрева) гомогенного двухфазного потока. Обозначим через Δp₀ сопротивление трения при x = 0.

Тогда

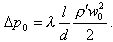
(8.55)

Для обогреваемого гомогенного потока в формуле (8.75) принимается среднеарифметическое значение x

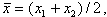
где x₁, x₂, - массовое паросодержание на входе и выходе участка трубы, тогда

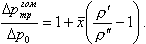
(8.56)

Для гомогенного потока сопротивление трения пропорционально массовому паросодержанию 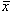(рис. 8.13).

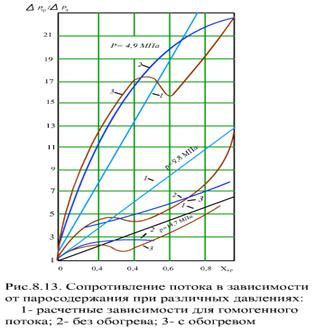
Экспериментальные данные, приведенные на этом же рисунке, показывают, что гидравлическое сопротивление трения в действительном двухфазном потоке существенно отличается от гомогенной модели. Это относится как к случаю с обогревом потока, так и к адиабатному потоку. Поэтому в расчетные формулы (8.55) и (8.56) вводится коэффициент ψ, учитывающий влияние структуры потока, и формулы приобретают вид:

при постоянном паросодержании

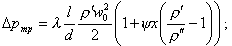
(8.57)

при переменном паросодержании

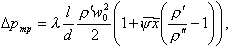
(8.58)

где 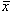- среднее паросодержание на участке,

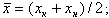
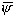- средний коэффициент, который определяется по формуле

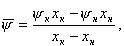
где ψ_Н, x_Н, ψ_К, x_К, относятся к начальному и конечному сечениям участка (трубы).

Коэффициент ψ зависит от скорости потока и его давления. Номограммы для определения ψ приведены в справочной литературе.

Интенсивность теплового потока q, кВт/м² или кВт/м длины, влияет на величину x_ср( 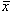), что учитывается при расчете Δp_ТР , и на структуру потока. При малых x_СР наличие обогрева трубы увеличивает сопротивление трения, а при больших x_СР - уменьшает. Влияние теплового потока q на сопротивление трения обычно невелико, сопоставимо с погрешностью определения сопротивления и при расчете Δp_ТР в явном виде на учитывается. Поэтому коэффициент ψ для обогреваемых труб прямоточных элементов котла определяется в зависимости от x_СР, массовой скорости ρw и давления р.

При расчете потерь давления в местных сопротивлениях Δp_М за основу принимается формула для гомогенного потока, аналогичная (8.54), а действительная структура потока учитывается введением условного коэффициента местного сопротивления ς_М

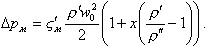
(8.59)

Расчет потерь давления от ускорения потока Δp_УСК производится по (8.14 в). Для двухфазного потока эту формулу можно привести к другому виду с учетом уравнения неразрывности

(ρw = ρ'w_СМ = w(1/v_СМ);

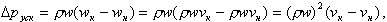
(8.60)

где v_Н и v_К - удельный объем теплоносителя в начале и конце участка (однофазного или двухфазного).

Удельный объем пароводяной смеси был ранее определен в (8.49 б).

Окончательно получим

(8.61)

При расчете нивелирного сопротивления (нивелирного напора) Δp_НИВ среднюю плотность двухфазного потока определяют по среднему значению истинного паросодержания

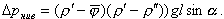
(8.62)

Для вертикальной трубы высотой Н

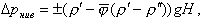
(8.63)

где знак” +” для подъемного, а “- “для опускного движения потока.

Для расчета составляющих перепада давления Δp необходимо знать конструктивные характеристики трубы, а также определить коэффициент трения ψ, коэффициент местного сопротивления ξ_М, ξ_М. Эти данные приведены в Нормативном методе гидравлических расчетов котельных агрегатов и соответствующих справочниках.