Уравнения неразрывности, движения, энергии и состояния жидкости.
Рассмотрим движение жидкости в обогреваемой трубе диаметром d (рис. 8.3). Считаем жидкость химически однородной, т.е. в ней нет примесей других веществ. Для описания состояния потока жидкости необходимо определить поля температуры Т, давления р и скорости W
Т = Т (x, y, z, t);
p = p (x, y, z, t);(8.1)
W = W (x, y, z, t),
где х, у, z - координаты; t - время.
Зная поля температуры, давления и скорости, можно рассчитать характеристики теплообмена и гидродинамики (тепловой поток, гидравлическое сопротивление и т.д.).
Поля температуры, давления и скорости называются стационарными, если T, р и W не изменяются во времени, или нестационарными, если зависят от времени.
Для определения Т, р и W используются уравнения неразрывности, движения и энергии. Эти уравнения получены из основных законов физики - закона сохранения массы, закона сохранения количества движения и закона сохранения энергии - с учетом специфических законов, характеризующих движение вязкой теплопроводной жидкости.
Запишем уравнения неразрывности, движения и энергии для одномерного потока (по оси z).
Уравнение неразрывности:
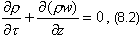
где ρ - плотность жидкости, зависящая от Т и р.
При стационарном движении ∂ρ/∂τ = 0 и уравнение неразрывности примет вид

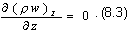
Таким образом, для установившегося движения при постоянном сечении трубы f, м2, и отсутствии притока (или оттока) жидкости получаем
ρw = const, (8.4)
т.е. массовая скорость потока ρw, кг/(м2·с), в указанных условиях есть величина постоянная.
Расход массы жидкости через трубу G, кг/с,
G = ρwf. (8.5)
Уравнение движения. Выделим из потока жидкости в трубе (рис. 8.3) двумя сечениями I и II, расположенными на расстоянии dz, элементарный объем движущейся жидкости dV = fdz. Применяя к нему теорему о количестве движения (изменение количества движения материальной системы равно сумме приложенных к системе внешних сил), запишем
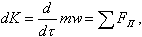 (8.6)
(8.6)
Для стационарного потока изменение количества движения dK массы жидкости, проходящей через сечение трубы l
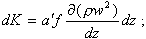 (8.7)
(8.7)
где a' - коэффициент, учитывающий неравномерность распределения скоростей по сечению трубы. Для развитого турбулентного потока а' ≈ 1.
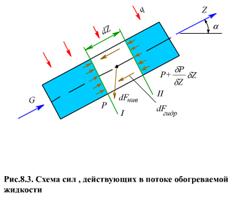
Внешними силами, приложенными к объему dV , являются силы давления потока, силы вязкостного сопротивления, силы земного притяжения. Изменение этих сил на элементе dz в проекции на ось z:
изменение силы давления
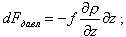 (8.8)
(8.8)
изменение сил вязкостного сопротивления (сил трения, сил гидравлического сопротивления) dFГИДР определяется касательным напряжением sСТ у стенки по экспериментальным данным
sСТ = λρw2/8,
где λ - коэффициент сопротивления трения.
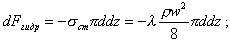
C учетом этого
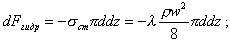 (8.9)
(8.9)
изменение сил земного притяжения (нивелирная составляющая)
 (8.10)
(8.10)
где α - угол между горизонталью и осью z (рис. 8.3).
Приравняв (8.7) к сумме (8.8), (8.9) и (8.10) и поделив обе части выражения на dz и , получим
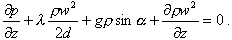 (8.11)
(8.11)
Уравнение (8.11) можно представить в виде дифференциального уравнения
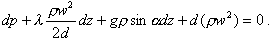 (8.12)
(8.12)
Интегрируя уравнение (8.12) с учетом (8.4), получаем формулу для расчета перепада давления на длине трубы
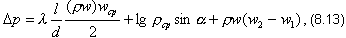
где ρСР (аналогично wСР) - среднеинтегральное значение плотности (скорости); w1, w2 - значения скорости в начале и конце участка трубы.
Выражение (8.13) обычно записывается в общем виде
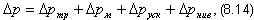
где Δpтр - сопротивление трения,
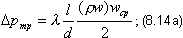
Δpм- местное сопротивление (сопротивление входа в трубу и выхода из нее, шайб, поворотов и т.п.),
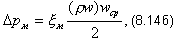
| (8.14б) |
где ξМ - коэффициент местного сопротивления; ΔpУСК - сопротивление ускорения,
| ΔpУСК = ρw(w2 - w1); | (8.14в) |
ΔpНИВ - нивелирное сопротивление,
| ΔpНИВ = glρСРsinα; | (8.14г) |
для вертикальной трубы при подъемном движении среды sin α = 1, при опускном движении sin α = -1
Дата добавления: 2015-07-10; просмотров: 2298;
