Уравнение энергии.

К потоку жидкости на участке dz подводится теплота Q_ВН в количестве

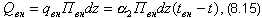
(8.15)

где q_ВН - плотность внутреннего теплового потока, кВт/м²; П_ВН внутренний периметр трубы, м; α₂- коэффициент теплоотдачи от стенки к потоку жидкости; t_ВН - температура металла на внутренней поверхности стенки, °С; t - средняя температура жидкости, °С.

Периметр трубы можно выразить через внутренний диаметр d_ВН, м, трубы

П_ВН = πd_ВН.

В (8.15) использовано уравнение теплоотдачи в виде

Количество теплоты, переносимой потоком жидкости, изменится на отрезке трубы длиной l

∂(ρh) /∂ l = 0

где h - энтальпия жидкости, кДж/кг.

Для установившегося потока уравнение (8.15) перепишем в другом виде

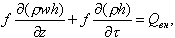
(8.17)

Учитывая, что для установившегося потока ∂(ρh)/∂τ = 0, получаем из (8.15) и (8.17)

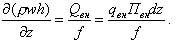
(8.18)

или

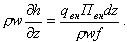
(8.19)

При q_ВН = const на участке трубы длиной dz изменение энтальпии потока жидкости

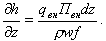
(8.20)

Обычно при расчете теплообмена в поверхностях нагрева парового котла задается (рассчитывается) тепловой поток с наружной поверхности трубы q_Н. Определение внутреннего теплового потока q_ВН с учетом аккумуляции теплоты в металле трубы определяется по формуле

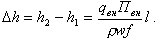
(8.21)

где П_Н = πd_Н - наружный периметр трубы, м; d_Н - наружный диаметр трубы, м; с_М - теплоемкость металла трубы, кДж/(кг·К);ρ_М- плотность металла, кг/м³; f_М - площадь поперечного сечения трубы по металлу, м²; t_М - средняя температура металла (по толщине стенки) трубы в данном сечении, °С.

В (8.21) произведение

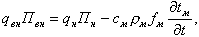
(8.22)

При стационарном режиме ∂t_м/∂τ = 0

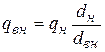
(8.23)

т.е. плотность теплового потока на внутренней поверхности трубы больше, чем на наружной поверхности в соотношении наружного и внутреннего диаметров b = d_Н/ d_ВН .

Уравнения состояния. При решении уравнений неразрывности, движения и энергии необходимо знать такие физические параметры жидкости, как плотность ρ, теплоемкость с_р, вязкость μ, теплопроводность λ и др.

Параметры ρ, c_p, μ, λ в общем случае зависят от температуры и давления. Эти зависимости выражают уравнения состояния, которые могут быть представлены в табличном, графическом виде или в виде формул. Для реальных жидкостей уравнения состояния основываются на экспериментальных данных.

При выводе уравнений неразрывности, движения и энергии не учитываются конкретные условия, в которых осуществляются движение жидкости и процесс теплообмена. Для решения задач о движении жидкости и теплообмене к основным уравнениям необходимо присоединить ряд условий, конкретизирующих задачу. Начальные условия состоят в задании полей скорости, температуры и давления во всем объеме рассматриваемой области (в том числе и на ее границах) в начальный момент времени. Начальные условия не задаются, если рассматривается стационарная задача.Граничные условия сводятся к заданию геометрической формы области и условий движения жидкости и теплообмена на ее границах.

Совокупность основных уравнений, уравнений состояния, начальных и граничных условий составляет замкнутую систему математического описания процесса движения жидкости и конвективного теплообмена в обогреваемых трубах.