Замена переменных в выражении, содержащем обыкновенные производные.
Пусть в дифференциальном выражении 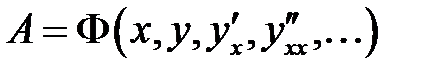 требуется перейти к новым переменным:
требуется перейти к новым переменным: 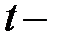 независимой переменной и
независимой переменной и 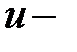 функции, связанным с прежними переменными
функции, связанным с прежними переменными 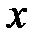 и
и 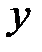 уравнениями
уравнениями
 . (7)
. (7)
Дифференцируя уравнение (7), будем иметь:
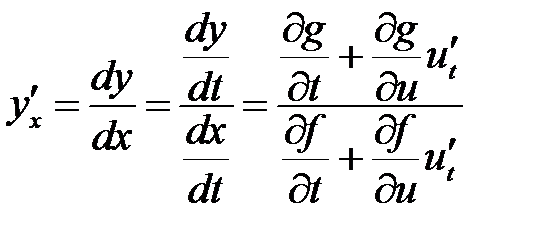 .
.
Аналогично выражаются высшие производные. В результате мы получаем
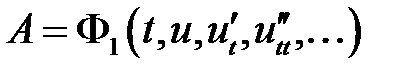 .
.
Пример 3. Преобразовать уравнение 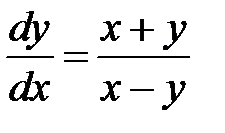 перейдя к полярным координатам
перейдя к полярным координатам 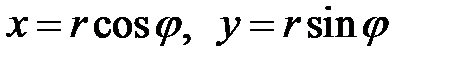 .
.
Решение.Рассматривая 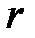 как функцию
как функцию 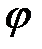 , получим
, получим
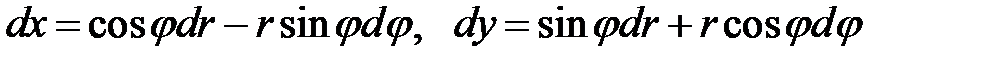 ,
,
отсюда
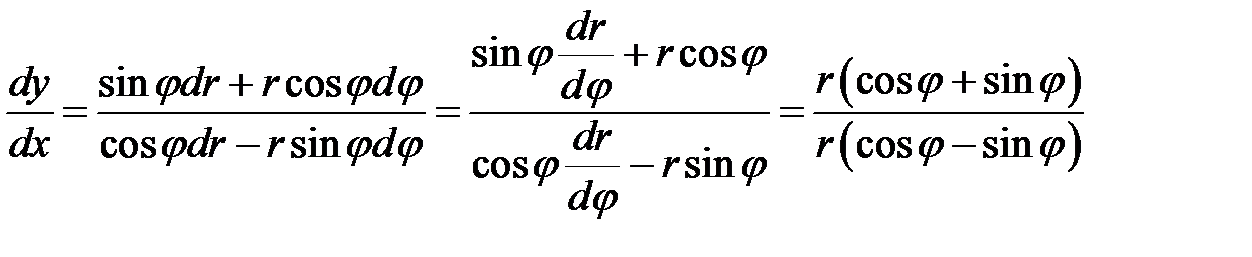 ,
,
или после упрощений 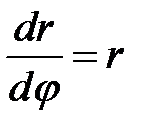 .
.
Пример 4. Преобразовать уравнение 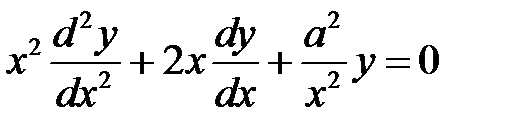 , полагая
, полагая 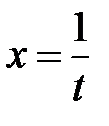
Дата добавления: 2015-08-11; просмотров: 2103;
