Производные и дифференциалы высших порядков.
Определение 1.Частная производная (если она существует) от частной производной первого порядка функции 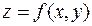 называется частной производной второго порядка.
называется частной производной второго порядка.
Дифференцируя 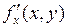 по
по 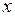 и по
и по 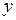 , получим две частные производные второго порядка, которые обозначаются следующим образом:
, получим две частные производные второго порядка, которые обозначаются следующим образом:
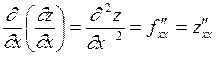 ,
, 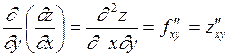 .
.
Аналогично для 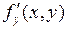 :
:
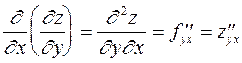 ,
, 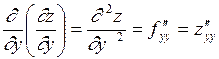 .
.
Производные 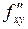 и
и 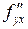 называются смешанными производными, они отличаются тем, что первая получена дифференцированием функции
называются смешанными производными, они отличаются тем, что первая получена дифференцированием функции 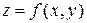 сначала по
сначала по 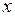 , а затем по
, а затем по 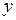 , вторая, наоборот, – сначала по
, вторая, наоборот, – сначала по 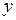 , затем по
, затем по 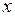 .
.
Аналогично определяются и обозначаются частные производные порядка выше второго.
Пример 3.Найти частные производные второго порядка функции 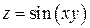 .
.
Решение. Находим сначала частные производные первого порядка:
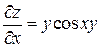 ,
, 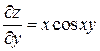 ,
,
а затем частные производные второго порядка:
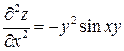 ,
, 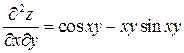 ,
,
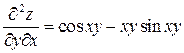 ,
, 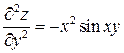 .
.
В примере 1 смешанные производные оказались тождественными, и это не случайно, так как имеет место следующая теорема.
Теорема 1. (о равенстве смешанных производных) Если функция 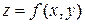 и ее частные производные
и ее частные производные 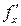 ,
, 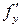 ,
,  ,
, 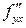 определены и непрерывны в точке
определены и непрерывны в точке  и в некоторой ее окрестности, то в этой точке справедливо равенство:
и в некоторой ее окрестности, то в этой точке справедливо равенство: 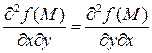 .
.
Если частные производные, подлежащие вычислению, непрерывны, то результат многократного дифференцирования не зависит от порядка дифференцирования.
Пример 4.Найти частные производные второго порядка от функции 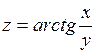 .
.
Дата добавления: 2015-08-11; просмотров: 494;
