Дифференцирование функции, заданной неявно.
Лекция № 5
1. Случай одной независимой переменной.Пусть уравнение 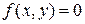 , где
, где 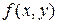 – дифференцируемая функция переменных
– дифференцируемая функция переменных 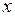 и
и 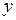 , определяет
, определяет 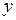 как функцию от
как функцию от 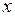 . Тогда производная этой неявно заданной функции при условии, что
. Тогда производная этой неявно заданной функции при условии, что 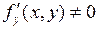 , может быть найдена по формуле
, может быть найдена по формуле 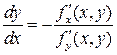 (1)
(1)
Пример 1.Найти 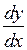 , если
, если 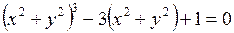 .
.
2. Случай нескольких независимых переменных.Пусть уравнение 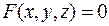 , где
, где 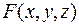 – дифференцируемая функция переменных
– дифференцируемая функция переменных 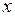 ,
, 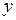 и
и 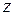 определяет
определяет 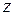 как функцию независимых переменных
как функцию независимых переменных 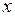 и
и 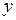 . Тогда, при условии что
. Тогда, при условии что 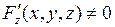 , частные производные этой неявно заданной функции могут быть найдены по формулам
, частные производные этой неявно заданной функции могут быть найдены по формулам 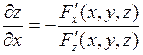 ,
, 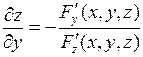 (2)
(2)
Другой способ нахождения производных функции 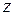 следующий: дифференцируя уравнение
следующий: дифференцируя уравнение 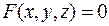 , получим
, получим 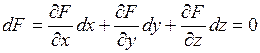 . Отсюда можно определить
. Отсюда можно определить 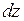 , а следовательно,
, а следовательно, 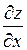 и
и 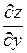 .
.
Пример 2. Найти 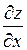 и
и 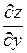 , если
, если 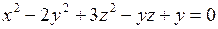 .
.
Решение.1-й способ. 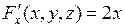 ,
, 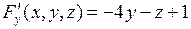 ,
, 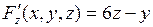 . Далее, применяем формулу (2), получим
. Далее, применяем формулу (2), получим 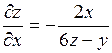 ;
;
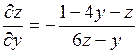 .
.
2-й способ. Дифференцируя данное уравнение, получим
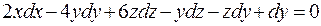 .
.
Отсюда 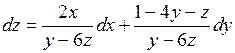 .
.
Дата добавления: 2015-08-11; просмотров: 661;
