Дифференциалы высших порядков.
Определение 2. Дифференциалом второго порядка функции 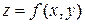 называют дифференциал от дифференциала (первого порядка) этой функции
называют дифференциал от дифференциала (первого порядка) этой функции 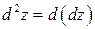 .
.
Аналогично определяются дифференциалы функции 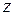 порядка выше второго, например
порядка выше второго, например 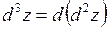 и, вообще,
и, вообще, 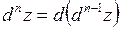 .
.
Если 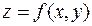 , где
, где 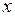 и
и 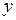 – независимые переменные и функция
– независимые переменные и функция 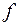 имеет непрерывные частные производные 2-го порядка, то дифференциал второго порядка функции
имеет непрерывные частные производные 2-го порядка, то дифференциал второго порядка функции 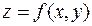 вычисляется по формуле
вычисляется по формуле
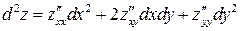 .
.
При наличии соответствующих производных справедлива символическая формула 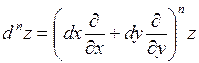 , которая формально развертывается по биномиальному закону.
, которая формально развертывается по биномиальному закону.
Если 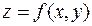 , где аргументы
, где аргументы 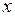 и
и 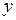 это функции одного или нескольких независимых переменных, то
это функции одного или нескольких независимых переменных, то
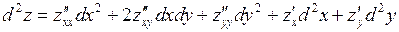 .
.
Если 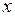 и
и 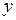 – независимые переменные, то
– независимые переменные, то 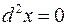 ,
, 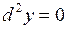 и формула (4) становится тождественной формуле (3).
и формула (4) становится тождественной формуле (3).
Пример 5. Найти полные дифференциалы первого и второго порядков функции 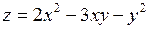 .
.
Для функции, заданной неявно производные высших порядков находятся последовательным дифференцированием формулы (2).
Пример 6. Найти 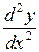 , если
, если 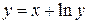 .
.
Пример 7.Найти 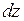 и
и  , если
, если 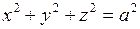 .
.
Дата добавления: 2015-08-11; просмотров: 729;
