Применим к (5.19) (5.11), тогда

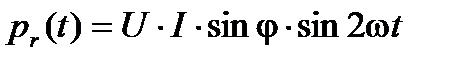(5.20)

Коэффициент

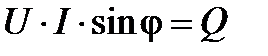[вар] (5.21)

называется реактивной мощностью, обозначается Q и измеряется в вольт-амперах реактивных [вар].

Теперь общее выражение для мгновенной мощности всей цепи (рис.3.1) можно записать в виде

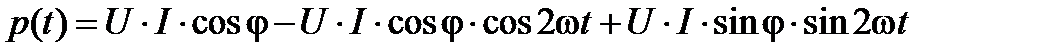(5.22)

Второе и третье слагаемые в (5.22) свернем как косинус суммы аргументов - 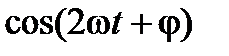. Тогда

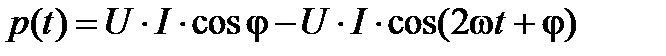(5.23)

Таким образом, мгновенная мощность цепи содержит постоянную и переменную составляющие. Переменная составляющая изменяется относительно постоянной с удвоенной частотой (рис.5.4). Амплитудное значение переменной составляющей обозначают S и называют полной мощностью цепи

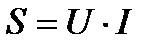[ВА]. (5.24)

Полная мощность в 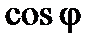раз превышает постоянную составляющую (активную мощность). Поэтому график мгновенной мощности заходит в область отрицательных значений. Величина области отрицательных значений определяется коэффициентом мощности. Физически эта область определяет моменты времени, в которые цепь возвращает энергию источника.

Если умножить все стороны треугольника сопротивлений (рис.3.2) на 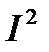, то получим треугольник мощностей (рис.4.5). В этом треугольнике гипотенуза - полная мощность S, прилежащей к острому углу катет - активная мощность Р, а противолежащий - реактивная мощность Q. Угол 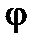определяется сдвигом фаз между током и напряжением цепи и задает значение коэффициента мощности. Для треугольника очевидны выражения

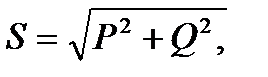(5.25)

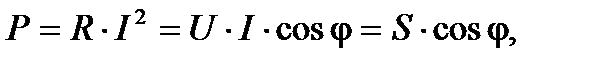
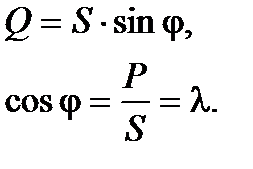(5.26)

Полная мощность S это теоретически достижимая, расчетная мощность, По значению S производятся расчеты сечения проводов, изоляции, параметры приемников электрической энергии. Из-за сдвига фаз 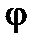мощность полностью не реализуется. Поэтому 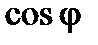и получил название коэффициента мощности. Всегда стремятся обеспечить его высоким.