Построение вложенных марковских цепей для моделирования систем при нелинейном изменении параметров потоков отказов и восстановлений программных средств
В соответствии с разработанной БММ 12 набор параметров модели следующий: λдп=var (изменяется при переходе из одного фрагмента в другой, т.к. Δλдп=var); μвп=var (изменяется при переходе из одного фрагмента в другой, т.к. Δμ=var). Этот вариант возможно описать набором выражений:
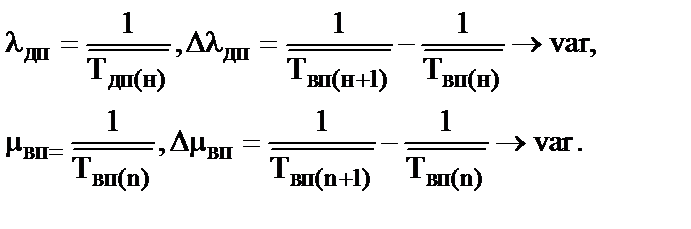 (3.31)
(3.31)
где Тдп(н) – среднее время между проявлениями ДП ПС;
Твп(n) – среднее время восстановления после проявления ДП ПС в одном из внутренних фрагментов.
Многофрагментный марковский граф СВГ S21 представлен на рис. 3.12.
Рис. 3.12 – Размеченный граф (ВМЦ) функционирования системы S21, построенный в соответствии с БММ 12
Логика функционирования системы подобна функционированию, описанному в предыдущих моделях. Основное отличие заключается в том, что параметры Δμвп и Δ λдп изменяются в каждом фрагменте.
СДУ Колмогорова, построенная для графа (рис. 3.12), имеет следующий вид:
для начального фрагмента Фн
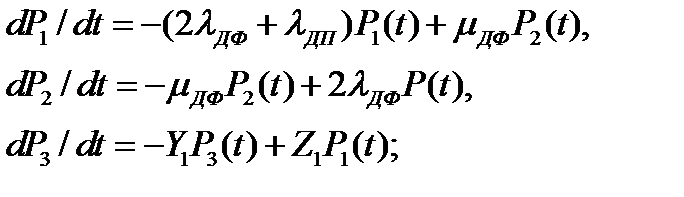
для внутренних фрагментов Фвн i
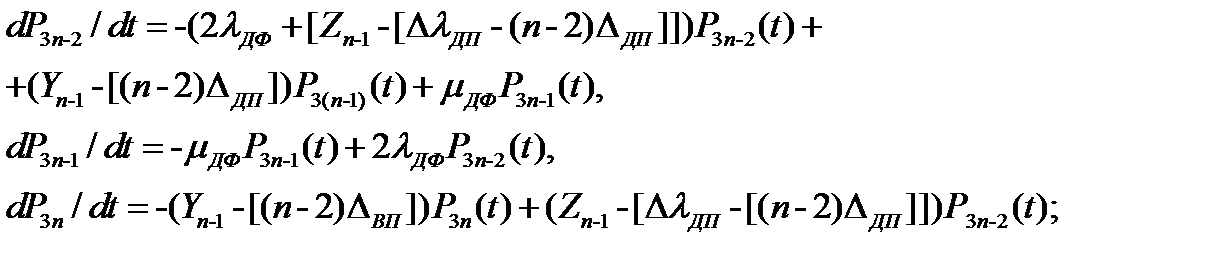 (3.32)
(3.32)
для конечного фрагмента Фк
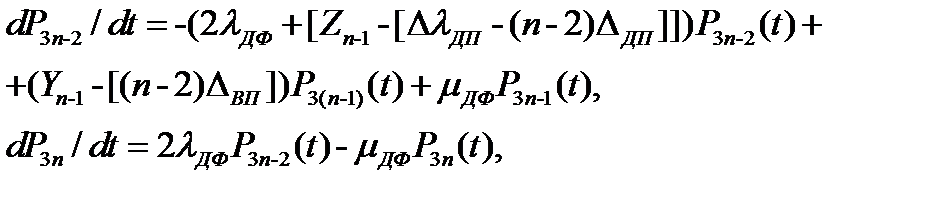
где Z1=λдп; Zn=Zn-1-[Δλдп-(n-2)Δдп] ; Y1=μвп; Yn=Yn-1-[(n-2)Δвп].
Функция готовности определяется по (3.21), а функция оперативной готовности – по (3.22).
Рассмотрим построение ВМЦ в соответствии с БММ 12 для СиТВГ с архитектурой S22.
Набор параметров модели следующий: λдп=var (изменяется при переходе из одного фрагмента в другой), Δλдп=var (изменяется в каждом внутреннем фрагменте); μвп=var (изменяется при переходе из одного фрагмента в другой) Δμвп=var (изменяется при переходе из одного внутреннего фрагмента в другой); λдп(1)=λдп(2), где λдп(1) и λдп(2) – интенсивности проявления ДП ПС программных версий V1 и V2; Λдп=λдп(1)+λдп(2) – суммарная интенсивность проявления ДП ПС.
Для построения многофрагментой марковской модели следует ввести допущение о том, что параметры, характеризующие восстановление ПС после проявления ДППС μвп(1), Δμвп(1) и Δвп(1) – первого информационного канала равны параметрам μвп(2), Δμвп(2) и Δвп(2) – второго информационного канала. Поэтому, в силу линейности разрабатываемой модели и для упрощения процесса моделирования возможно введение нового параметра Μвп – суммарной интенсивности восстановления после проявления ДП ПС:
Μвп=μвп(1) + μвп(2).
Следует отметить, что введение таких допущений не позволяет учесть особенности восстановления ПС разных информационных каналов, однако, на первом этапе, позволяет учитывать изменение времени при проведении процедур восстановления после проявления различных ДП ПС.
Многофрагментный марковский граф СВГ S22 представлен на рис. 3.13.
Рис. 3.13 – Размеченный граф (ВМЦ) функционирования системы S22, построенный в соответствии с БММ 12
Логика функционирования системы состоит в следующем. В начальный момент времени система реализует все предписанные функции и находится в состоянии S1. В следующий момент времени проявляются ДП ПС или возникают ДФ АС. При возникновении ДФ АС система переходит в состояние S2 c интенсивностью 2λдф. Далее с интенсивностью μдф система восстанавливается. При проявлении ДП ПС система переходит в состояние S3 и с интенсивностью Mвп восстанавливается (состояние S4). В соответствии с принятым вариантом во внутренних фрагментах параметры μвп и Λдп изменяются на величины Δμвп.и Δλдп. Кроме того в каждом внутреннем фрагменте параметры Δμвп.и Δ λдп изменяются на величины Δдп и Δвп. Параметр Mвп линейно уменьшается до величины μвп(min). Это значение определяется максимально допустимым временем восстановления ПС.
СДУ Колмогорова, построенная из графа (рис. 3.13) имеет следующий вид:
для начального фрагмента Фн
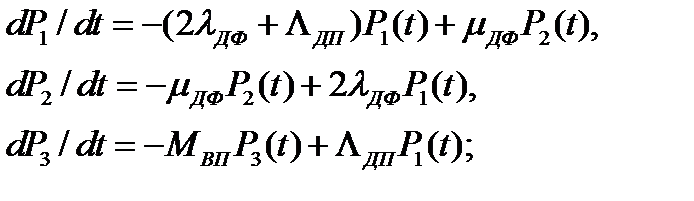
для внутренних фрагментов Фвн i
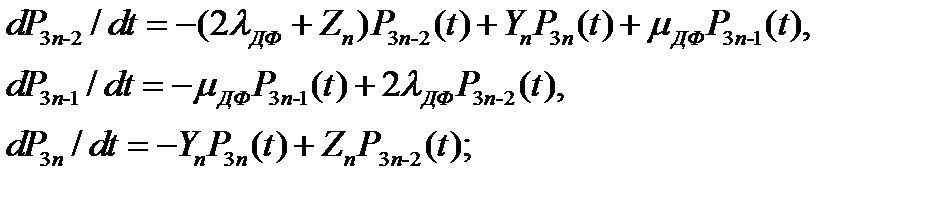 (3.33)
(3.33)
для конечного фрагмента Фк
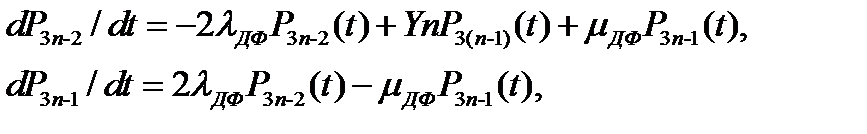
где Zn=Zn-1–[Δλдп–(n–2)Δдп] – интенсивность проявления ДП ПС n-го фрагмента;
Yn=Yn-1–[Δμвп–(n–2)Δвп] – интенсивность восстановления после проявления ДППС (n+1) – го фрагмента.
Функция готовности определяется по (3.21), а функция оперативной готовности – по(3.22).
Анализ моделей показывает рост размерности решаемых задач, связанных с усложнением рассматриваемых структур систем, что приводит к увеличению размерности матрицы СДУ Колмогорова. Так, для ВМЦ, построенной для архитектуры СВГ Sк22 на основе БММ 1, количество состояний зависит от числа невыявленных дефектов ПС и указано в таблице 3.4.
Таблица 3.4 – Зависимость количества фрагментов и состояний графа ВМЦ, построенной для архитектуры СВГ Sк22 на основе БММ 1
| Число фрагментов | Число состояний в фрагменте | Nдеф=6 | Nдеф=50 |
| Фн=1 | |||
| ФI=1 | |||
| ФII=N-2 | |||
| ФIII=2 | |||
| ФIV=N-6 | |||
| ФV=2 | |||
| Фпредп.=1 | |||
| Фк=4 | |||
| Всего фрагментов | |||
| Всего состояний |
Следовательно, для решения СДУ целесообразней применять численные методы [24], а выбор конкретного метода решения следует осуществлять с учетом жесткости параметров рассматриваемых систем.
Дата добавления: 2015-08-11; просмотров: 1058;
