Основы теории тарельчатого клапана
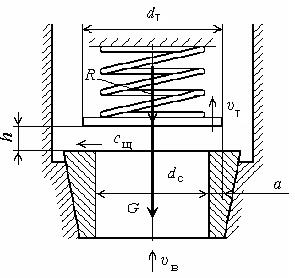
Рассмотрим работу тарельчатого клапана поршневого или плунжерного насоса (рис. 17). Пусть тарелка клапана поднимается с некоторой скоростью υт. Количество жидкости, проходящей через отверстие седла клапана, будет равно количеству жидкости, проходящему через щель, которая образуется между тарелкой и седлом, плюс объем (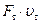 
), освобождаемый тарелкой клапана при своем подъеме вверх.
Площадь щели у открытого тарельчатого клапана с плоской тарелкой будет равна:
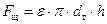, (38)
где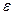 
- коэффициент сжатия струи в щелевом зазоре; 
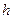- высота подъема тарелки клапана над седлом; dт – диаметр тарелки.
На основании сказанного можно записать
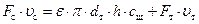, (51)
где 
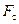- площадь поперечного сечения отверстия седла клапана; 
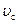- средняя ско-
рость жидкости в седле клапана;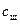 
- скорость жидкости в щелевом зазоре между тарелкой и седлом клапана.
При опускании тарелки выражение (51) запишется в виде
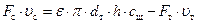. (52)
Рис. 18. Схема тарельчатого клапана.
Если принять направление движения тарелки клапана вверх положительным, а вниз – отрицательным, то общее выражение для подъема и опускания тарелки клапана запишется в виде (закон Вестфаля):
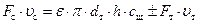. (53)
Из (53) определим высоту подъема тарелки клапана:
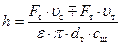. (54)
Уравнение постоянства расхода жидкости, движущейся в цилиндре и в отверстии седла клапана, можно записать как:
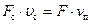, (55)
где vп– скорость поршня (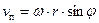 
).
Запишем выражение (55) с учетом выражения для скорости поршня
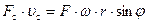. (56)
Тогда уравнение (54) примет вид:
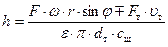. (57)
Найдем скорость подъема тарелки клапана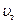 
. Для этого продифференцируем выражение (54) по времени:
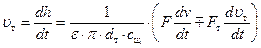. (58)
Если в выражении (58) отбросить член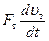 
, который в сравнении с 
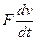составляет малую величину более высокого порядка, то выражение для определения 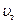примет вид
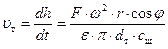. (59)
Так как тарелка клапана движется неравномерно, то на тарелку будет действовать сила инерции, которую обычно в расчетах не учитывают вследствие её малой величины.
Уравнение равновесия сил, действующих на тарелку клапана, имеет вид:
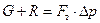. (60)
где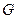 
- сила тяжести тарелки клапана в жидкости; R – сила сжатия пружины; 
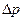- разность давлений над и под тарелкой клапана.
Разделив правую и левую часть уравнения (60) на (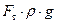 
) получим: 
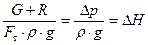, (61)
где ∆H – потери напора на клапане.
Применив известную из гидравлики зависимость для определения скорости истечения жидкости из отверстия или насадка, определим скорость истечения жидкости из щелевого зазора между тарелкой и седлом клапана:
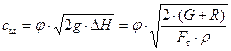, (62)
где φ – коэффициент скорости щелевого зазора.
Зависимость для определения высоты подъема тарелки клапана, с учетом выражений (57), (59) и (62) примет вид:
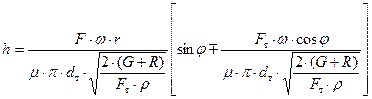, (63)
где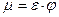 
– коэффициент расхода клапана.
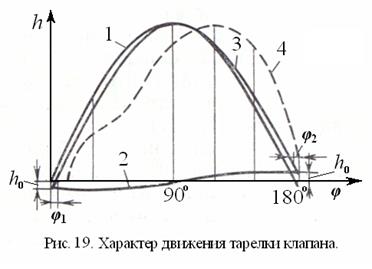На рис. 19 показан графический вид зависимости (63). Синусоида 1 построена с использованием первого члена правой части уравнения (63), а косинусоида 2 – с использо-ванием второго члена этого же уравнения. Путем суммиро-вания ординат синусоиды 1 и косинусоиды 2 построена кривая 3, выражающая характер движения тарелки клапана, то есть изменение высоты её подъема в зависимости от угла поворота кривошипа. Кривая 3 указывает на несоответствие моментов открытия и закрытия клапана крайним положениям поршня. После того как кривошип повернется на угол φ1, тарелка клапана начинает подниматься. Кривошип повернулся на 1800, а клапан ещё открыт и тарелка находится на расстоянии h0 от опорной поверхности седла. После поворота кривошипа на угол (1800+ φ2) произойдет закрытие клапана.
Угол φ1 – угол запаздывания клапана при открытии, а φ2 – угол запаздывания клапана при закрытии.
Углы запаздывания φ1 и φ2 можно определить при помощи той же зависимости (63). Клапан откроется при повороте кривошипа на угол φ1, определяемый из условия, что при φ = φ1 h = 0.
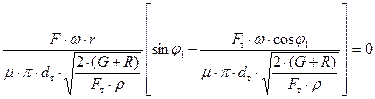. (64)
Ни один из параметров, входящих в множитель перед квадратными скобками, при работе насоса не равен нулю; нулю может быть равно только выражение в квадратных скобках:
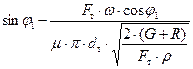= 0, или 
,
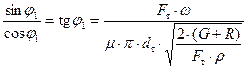отсюда
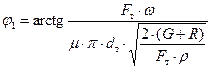. (65)
Такую же зависимость получим и для угла φ2, однако в действительности φ1 и φ2 могут быть разными по величине.
Для клапана с плоской тарелкой (см. рис. 47) при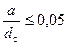 
(а – ширина опорной поверхности; 
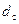- диаметр отверстия седла) С.Н. Рождественский рекомендует использовать следующую формулу для определения коэффициента расхода:
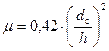. (66)
Однако эта формула пригодна лишь для квадратичного режима движения жидкости через отверстие седла, а этот режим имеет место при Reщ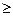 
10.
Здесь число Рейнольдса потока у входа в щель
Reщ=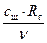 
, (67)
где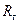 
- гидравлический радиус щели, определяемый по формуле:
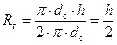. (68)
С учетом зависимости (68) выражение (67) запишется в следующем виде:
Reщ=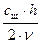 
. (69)
Для конических тарельчатых клапанов с углом конусности β=450 С. Н. Рождественский рекомендует формулу
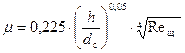. (70)
Эта формула справедлива при числах Рейнольдса 25<Reщ<300.
Для кольцевых клапанов с плоской тарелкой и узкой опорной поверхностью О.В. Байбаков рекомендует следующую формулу для определения коэффициента расхода:
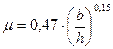, (71)
где b – ширина прохода в седле клапана.
Формула (71) справедлива для Reщ<10.
Максимальный подъем тарелки клапана будет при φ = 900, тогда зависимость (63) примет вид
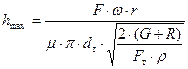. (72)
Из рис. 19 (линия 4) видно, что hmax имеет место, когда поршень пройдет путь больше, чем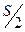 
, то есть в результате большего сопротивления отрыву тарелки от седла открытие происходит с рывком. Под действием силы инерции тарелки клапана её подъем происходит со скорость, превышающей скорость поршня в данном положении. Вследствие этого при дальнейшем подъеме тарелки клапана её скорость уменьшится и подъем будет более плавным. Об этом свидетельствует более пологий участок кривой.
Когда клапан открыт и через него протекает жидкость, гидравлические потери в нем определяют по формуле:
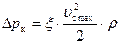, (73)
где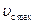 
- максимальная скорость жидкости в отверстии седла клапана; 
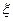- коэффициент гидравлического сопротивления клапана.
Опытами установлено, что гидравлические потери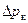 
сравнительно мало меняется от высоты подъема тарелки клапана. Небольшое уменьшение 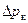происходит в период опускания тарелки клапана, то есть тогда, когда это не имеет практического значения для определения давления под клапаном. Поэтому величину 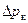рекомендуется определять для среднего положения поршня, когда 
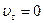и h=hmax.
В выражении (61) скорость 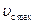выразим через скорость поршня v:
.
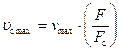Тогда формулу (73) следует записать в виде
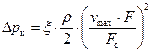, (74)
Коэффициент гидравлического сопротивления 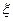зависит от конструкции клапана.
Для определения коэффициента 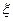известны следующие эмпирические формулы Баха:
1. Для тарельчатого клапана с плоской тарелкой без нижнего направления
(75)
где a – ширина поверхности соприкосновения тарелки и седла клапана;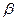 
– опытная величина, которая находится в пределах 0,15 – 0,16; dс - диаметр отверстия седла клапана; h - высота подъема тарелки клапана.
Величину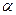 
рекомендуется определять по формуле:
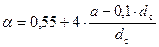(76)
При пользовании формулами (75) и (76) должны быть выполнены следующие соотношения между размерами h, dс и a: 4<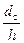 
<10, 4 a< dс<10 a.
2. Для тарельчатого клапана с плоской тарелкой и нижними направляющими в виде ребер:
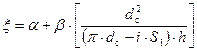; (77)
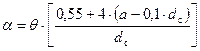, (78)
где 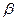– величина, равная 1,70÷1,75; 
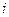- число ребер; 
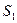- ширина ребра; 
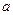- ширина поверхности соприкосновения тарелки и седла клапана.
Величину коэффициента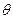 
выбирают в зависимости от степени стеснения ребрами площади поперечного сечения отверстия седла 0,8≤ 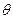<1,6;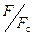 
=0,80 ÷ 0,87, где F - площадь поперечного сечения ребер тарелки клапана; Fс – площадь отверстия седла клапана.
3. Для тарельчатого клапана с конусной опорной поверхностью и верхним направляющим в виде стержня
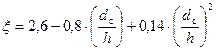. (79)
При пользовании эмпирической формулой (59) должны выполняться следующие условия: 4<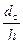 
<10;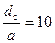 
.
Дата добавления: 2015-07-10; просмотров: 1175;