Общие сведения; образование критериальных уравнений и критериев подобия для насосов; коэффициент быстроходности насосов ns.

ОСНОВЫ ТЕОРИИ ПОДОБИЯ НАСОСОВ.

Общие сведения. Теория подобия создавалась для накопления и хранения экспериментальных данных, а также для их использования на объектах, подобных между собой. Во все времена перед созданием достаточно крупного и ценного изделия старались сделать его уменьшенную копию, модель. По свойствам этой модели пытались предсказать свойства натурного объекта с учётом подобия модели и натуры. На этом пути проявился ряд достаточно любопытных особенностей и закономерностей, на основе которых и была разработана теория подобия в её настоящем виде. В частности, для насосов было установлено, что при полном геометрическом подобии модель, уменьшенная в два раза, при работе на подобном режиме, потребляла мощность не в два, не в четыре, а в 32 раза меньше, чем соответствующий натурный объект. Из примера видно, что использование простых аналогий в деле моделирования поведения подобных объектов невозможно. Кроме того, в примере использовано понятие «подобный режим», которое здесь логически необходимо, но требует специального пояснения. Отмеченные особенности и наиболее важные закономерности использования теории подобия достаточно просто объясняются из рассмотрения её основ.

Теория подобия рассматривает три вида подобия: геометрическое, кинематическое и динамическое.

Геометрически подобными считаются объекты, у которых равны сходственные углы и пропорциональны сходственные размеры.

Кинематическое и динамическое подобия рассматривается применительно к потокам жидкости. Кинематически подобными считаются потоки, текущие в геометрически подобных каналах, в сходственных точках которых треугольники скоростей подобны.

Динамически подобными считаются потоки, которые текут в геометрически подобных каналах, в сходственных точках которых многоугольники внешних сил подобны.

Для насосов достаточно обеспечить кинематическое подобие, чтобы автоматически выполнялось и динамическое подобие.

Насосы считаются подобными и работающими на подобных режимах, если в таком случае удовлетворяются все виды подобия.

Теория подобия, будучи созданной для определения соотношений параметров между подобными объектами, использует математический аппарат, в котором действуют не обычные, а относительные или безразмерные параметры. Эти безразмерные параметры получаются как соотношения размерных величин. Существует два вида безразмерных параметров теории подобия: симплексы подобия и комплексы подобия. Симплексы образуются отношением одноимённых величин, например, коэффициент геометрического подобия и коэффициент сужения лопасти вычисляются по выражениям:

.

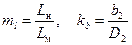Комплексы образуются комбинацией разноимённых величин, в результате чего образуются безразмерные величины, например известные критерии Рейнольда и Эйлера образуются по таким формулам:

.

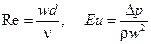Комплексы, в свою очередь, принято делить на числа и критерии. Числами называют комплексы, выступающие в роли функций, а критериями – комплексы, выступающие в роли аргументов. Соответственно один и тот комплекс может называться числом или критерием, в зависимости от того, в качестве какого параметра он входит в рассматриваемую зависимость.

В практике использования теории подобия также существует подход, при котором все безразмерные параметры теории подобия, независимо от способа образования и применения, иногда называются критериями, когда о них говорят в общих рассуждениях, не выделяя их особенности.

Уравнения, полученные в виде зависимостей между безразмерными параметрами, называются критериальными уравнениями. Существует два способа образования критериальных уравнений и вместе с ними критериев подобия. Первый основан на так называемой π-теореме анализа размерностей, а второй – на π-теореме анализа уравнений.

Первый способ используется в случае, когда исследуется объекты или явление, которые ещё не получили достаточного математического описания, и когда закономерности их поведения и взаимосвязи основных параметров определяются из эвристических предположений. В этом случае вначале образуют список основных параметров, между которыми, по мнению исследователя, необходимо установить взаимосвязь, а затем из этих параметров образуют симплексы и комплексы подобия, руководствуясь тем, чтобы все они не имели размерностей. Далее стараются экспериментально определить взаимное влияние между образованными безразмерными параметрами. Существует правило теории подобия, по которому полное число безразмерных параметров, описывающих искомую зависимость, не должно быть меньше, чем число соответствующих основных размерных параметров, между которыми устанавливается взаимосвязь. Следует иметь в виду, что влиянием отдельных параметров, как размерных, так и безразмерных, при практическом использовании образуемых зависимостей всегда можно пренебречь, если в рассматриваемом диапазоне их изменения это влияние практически не ощущается или ощущается очень мало. С учётом такого обстоятельства критериальное уравнение может быть существенно упрощено и сводиться к взаимосвязи двух или трёх комплексов, что позволит учитывать (с определёнными погрешностями) взаимное влияние всех входящих в эти комплексы параметров.

Очень важным при рассмотрении теории подобия является следующее положение: если рассматриваемые объекты подобны и работают на подобных режимах, то для этих объектов должно соблюдаться равенство всех критериев подобия, определяющих основные взаимосвязи между параметрами рассматриваемых объектов. Одновременно действует и положение, обратное ранее сформулированному: если для рассматриваемых объектов, работающих на сравниваемых режимах, имеет место равенство всех критериев подобия, то эти объекты подобны и работают на подобных режимах.

Приведенные положения могут рассматриваться в полной мере, с рассмотрением всех возможных критериев, определяющих рассматриваемые взаимосвязи, и в приближённых оценках, когда рассматривается равенство только основных критериев или тех, которые оказывают достаточно ощутимое влияние при анализе названных взаимосвязей.

Рассмотрим образование критериальных уравнений и критериев подобиядля насосов на основе π-теоремы анализа уравнений. С этой целью установим соотношение расходов жидкости через рабочие колёса сравниваемых (натурного, индекс «н», и модельного, индекс «м») насосов. Расходы через рабочие колёса больше, чем расходы через сами насосы из-за наличия внутренних протечек и равны G_р. Запишем уравнения расхода для рабочих колёс обоих насосов

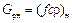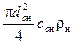= , (5.1)

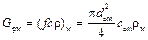. (5.2)

При делении (5.1) на (5.2) следует определиться со значениями отношений размеров, скоростей и плотностей жидкости. Соотношения одноимённых размеров для подобных насосов есть величина постоянная и равная геометрическому коэффициенту подобия m_l

.

Из записанного выше равенства также следует, что при постоянном m_L будет постоянным и отношение ширины лопасти на выходе к наружному диаметру колеса для подобных насосов, т.е.

= const.

где k_b – симплекс подобия, выделяемый в классической теории подобия насосов.

При определении соотношений одноимённых скоростей следует учитывать, что они являются одноимёнными сторонами подобных треугольников (в соответствии с кинематическим подобием). В этом случае можно записать:

,

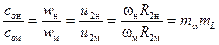где m_ω есть соотношение угловых скоростей роторов модели и натуры.

С учётом полученных отношений, можно записать отношения расходов модельного и натурного объектов в виде следующего выражения:

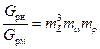, (5.3)

где m_ρ – соотношение плотностей в модельном и натурном насосах.

Учитывая возможность представления коэффициентов подобия в (5.3) в виде соотношений различных одноимённых величин, можно переписать (5.3) в таком виде:

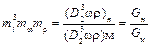. (5.4)

Если принять, что оба насоса работают на жидкости с одинаковой плотностью, то из (5.4) следует:

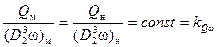. (5.5)

Коэффициент k_Qω, как это следует из (5.5), будет постоянным для подобных насосов, работающих на подобных режимах. Он называется коэффициентом подачи насоса, не имеет размерности и является принятым в теории подобия насосов критерием (комплексом) подобия, который пропорционален критерию Струхаля, известному в гидромеханике.

Если учесть, что расходы насосов G связаны с расходами через их колёса G_р через объёмные КПД насосов, η_о, то на основании (5.3) можно записать

. (5.6)

Определим далее соотношения между удельными работами подобных насосов, работающих на подобных режимах. Для теоретических удельных работ таких насосов можно записать:

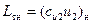_, (5.7)

. (5.8)

При делении (5.7) на (5.8) будем учитывать, что отношения двух одноимённых скоростей подобных насосов могут быть заменены отношением двух других одноимённых скоростей, поскольку подобие режимов предполагает подобие треугольников скоростей и пропорциональность сходственных сторон. Тогда

. (5.9)

На основании (5.9) можно записать ряд выражений.

Во-первых, из (5.9) следует, что

.

Коэффициент k_L здесь является общепринятым для теории насосов критерием подобия и носит название коэффициента удельной работы насоса. Этот коэффициент практически не отличается от критерия Эйлера, используемого в гидромеханике, и равного

.

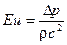Тождественность этих критериев можно объяснить, если учесть, что в соответствии с интегралом Бернулли 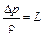, а скорость c является так называемой характерной скоростью, которую выбирают в зависимости от особенностей рассматриваемого объекта. С учётом отмеченного выше идентичность коэффициента k_L и критерия Eu очевидна.

Во-вторых, помимо критерия k_L на основании (5.9) могут быть получены родственные ему критерии. В частности, если заменить отношения выходных диаметров отношением диаметров входа, что справедливо при наличии геометрического подобия, то справедливо

и тогда верно

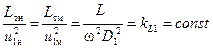. (5.9.а)

Критерий k_L1 эквивалентен критериям k_L и Eu, но характеризует течение потока в области входа насоса.

В-третьих, если учесть, что , то из (5.9) получим:

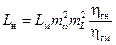. (5.10)

Определим соотношения мощностей подобных насосов, работающих на подобных режимах. Для обоих насосов запишем:

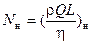(5.11)

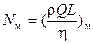(5.12)

При делении (11) на (5.12) получим:

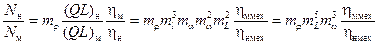. (5.13)

где η_ммех , η_нмех – механические КПД подобных насосов.

Из (13) следует:

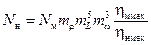. (5.14)

Если в соответствии с теорией подобия рассматривать один и тот же насос, работающий на различных режимах, то можно определить, какие из режимов можно считать подобными. Эти режимы интересны тем, что для них, в соответствии с отмеченными ранее положениями теории подобия, должно обеспечиваться равенство всех критериев подобия. В качестве таковых можно рассматривать объёмный и гидравлический КПД насоса, которые также являются безразмерными критериями подобия. Для одного и того же насоса m_L, m_ρ = 1. В этом случае можно определить расходы, удельные работы и мощности для подобных режимов работы насоса, по которым и можно идентифицировать искомые подобные режимы. Эти параметры считаются по формулам:

,

,

.

Из записанных выражений также следует, что для подобных режимов значения отношений

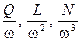
будут одинаковыми.

Таким образом, на основе всего изложенного можно представить основные возможности теории подобия в отношении образования критериев подобия и установления некоторых зависимостей между параметрами модельного и натурного насосов.

Для практического использования теории подобия при проектировании насосов весьма важно рассмотрение такого критерия, как коэффициент быстроходности насосовn_s.Этот критерий может быть образован из самых основных параметров насоса на основе уже рассмотренных подходов, в связи с чем изложение методики его определения здесь опускаем. Он определяется из выражения:

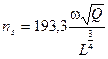. (5.15)

Данный критерий подобия имеет численный коэффициент, который совершенно не обязателен с точки зрения теории подобия. Тем не менее этот коэффициент необходим и его присутствие объясняется историческими причинами. В своё время критерий n_s содержал вместо ω и L родственные и однозначно связанные с ними параметры n и H – частоту вращения и напор. Соответственно в то время вместо международной системы единиц СИ использовалась техническая система единиц, МКГСС. Тогда же коэффициент быстроходности получил условную размерность (об/мин), присвоенную ему на достаточно спорных основаниях. В таком виде критерий всё равно отвечал всем условиям образования и использования критериев подобия и получил широкое применение в целом ряде эмпирических зависимостей, использовавшихся при проектировании насосов. Эти зависимости оказалось возможным использовать и в настоящее время при условии, что численное значение n_sсохранится неизменным при изменении системы размерностей. Именно для того, чтобы значение n_s осталось постоянным при смене системы размерностей и было введено число 193,3, которое выполняет в данном случае роль выравнивающего коэффициента.

Использование критерия n_s связано с основными положениями теории подобия, сформулированными ранее. Согласно им равенство определяющих критериев подобия при геометрическом подобии насосов означает, что рассматриваемые насосы можно рассматривать как работающие на подобных режимах и что для них будут равны прочие критерии подобия, в том числе их КПД.

Использование n_s в расчётной практике базируется на обобщении большого числа экспериментальных данных для различных насосов с хорошо доведенными рабочими процессами (с высокими КПД). Для этого в каждом случае, для каждого насоса (их можно назвать эталонными), были определены значения КПД и n_s. Далее были установлены зависимости для КПД и некоторых других критериев от критерия n_s в пределах отдельных диапазонов значений n_s. В частности, для центробежных насосов с этой целью было выделено три диапазона в общем диапазоне n_s от 40 до 300.

Располагая такими зависимостями, проектант нового насоса мог определить возможные значения КПД своего насоса, а также ряд дополнительных параметров, необходимых при его проектировании. С этой целью на основании основных исходных данных вначале определяется значение n_s для проектируемого насоса. После этого проектируемый насос рассматривается как подобный эталонному насосу с одинаковым n_s. На основании вычисленного n_s по располагаемым зависимостям определялись значения КПД, которые, в соответствии с теорией подобия, могли считаться равными для эталонного и проектируемого насоса. Аналогично определялись значения ряда других критериев, используемых при проектировании. Одновременно для проектируемого насоса вычислялись такие геометрические пропорции, которые обеспечивали его подобие с эталонным насосом. Определение геометрических пропорций также выполнялось в функции вычисленного значения n_s.

Следует отметить, что вычисленные на описанной основе КПД могут соответствовать реально обеспеченным значениям для спроектированного насоса только в том случае, когда при изготовлении и эксплуатации такого насоса будут в полной мере соблюдены все условия подобия, в том числе и условия одинаковой чистоты рабочих поверхностей, которые так или иначе подразумеваются при определении подобий конструкций и режимов.

Помимо уже рассмотренных аспектов применения теории подобия важно упомянуть и такой аспект, в соответствии с которым эта теория позволяет выбрать наилучший тип насоса в зависимости от сочетания его основных параметров, которые в таком случае выражаются через критерий n_s. При решении этой задачи на основе теории подобия рассматривались все возможные типы насосов, в результате чего были получены обширные базы данных, на основании которых были разработаны достаточно широкие рекомендации, в том числе и выходящие за рамки данного курса. Одним из результатов анализа собранного статистического материала была разработка классификации насосов в зависимости от численного значения критерия n_s. На рис. 5.1 приведена таблица, в соответствии с которой классифицируются лопастные насосы. В ней же приведены сведения по геометрическим пропорциям основных размеров колёс насосов для каждого выделенного диапазона значений n_s.

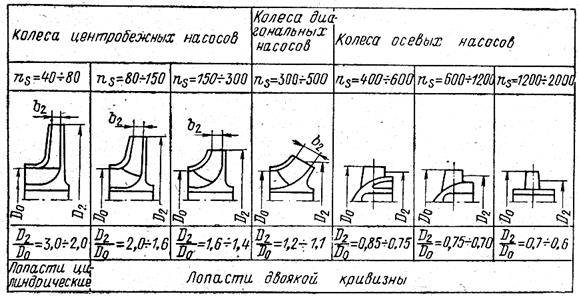
Рис. 5.1. Классификация насосов по n_s

Из выражения (5.15) следует, что при постоянной угловой ско­рости увеличение подачи и уменьшение удельной работы приводят к уве­личению коэффициента быстроходности насоса. Поэтому насосы с высокими n_s предназначаются для создания малых удельных работ и больших подач, а насосы с малыми n_s используются для больших удельных работ и малых подач.

Коэффициент быстроходности насоса при постоянных значе­ниях подачи и удельной работы изменяется прямо пропорционально угло­вой скорости. Увеличение угловой скорости приводит к уменьше­нию размеров и массы насоса. Поэтому выгодно на этой основе увеличивать ко­эффициент быстроходности насосов.

Рабочие колеса центробежных насосов с низкими n_s имеют длинный и узкий межлопастной канал и характеризуются отно­шением D₂/D₀ = 2,0…3,0. Лопасти таких колес выполняют ци­линдрическими. Жидкость в межлопастных каналах имеет зна­чительное радиальное перемещение. Колеса развивают большие напоры при небольших подачах.

Ограниченность применения тихоходных насосов с n_s < 50 свя­зана с быстрым ростом потерь от трения наружной поверхности колеса о жидкость и от трения жидкости при движении ее в кана­лах колеса. Коэффициент полезного действия получается низким.

Колеса насосов с n_s = 80…150 имеют более широкий канал и характеризуются отношением D₂/D₀ = 2,0…1,6. Лопасти колес насосов c n_s > 100 выдвинуты в область поворота потока из осе­вого направления в радиальное; на входе лопасть выполняется двоякой кривизны, а на выходе – цилиндрической.

При рассмотрении рис.1.5 следует иметь в виду, что цилиндрическими называют лопасти, имеющие одинарную кривизну. Образующая этих лопастей имеет вид прямой, параллельной оси вращения колеса. Входная кромка лопастей таких насосов начинается за поворотом потока из осевого направления в радиальное. Входные кромки лопастей двоякой кривизны выдвигаются в область поворота потока. В области входа эти лопасти получают отгиб в радиальном направлении. Построение такого участка лопасти подробно рассмотрено в теории центробежных компрессорных машин. Обычно за областью входа лопасти при n_s < 300 выполняются одинарной кривизны. При бóльших значениях n_s лопасти могут иметь двоякую кривизну на большей части длины, что учитывает особенности течения жидкости в межлопаточном канале таких насосов.

Следует подчеркнуть, что классификация насосов по n_s охватывает все типы насосов, а не только представленные в таблице 1.5. В соответствии с разработанной классификацией насосов в зависимости от n_s, насосы, имеющие n_s < 12 следует выполнять объемного типа, чтобы обеспечить высокие энергетические показатели таких насосов. В диапазоне между 12 и 40 наилучшие показатели обеспечивают насосы вихревого типа. При более высоких n_s рекомендуется применять лопастные насосы разных типов в соответствии с рис. 1.5.

Таким образом, в изложенной лекции рассмотрен один из специфических элементов теории проектирования насосов – теория подобия применительно к расчётам насосов. Как следует из лекции, она опирается на использование ряда основных критериев подобия, среди которых коэффициент быстроходности n_s является наиболее применяемым. Без него практически невозможно выполнить проектирование нового насоса, поскольку на его основе выполняется выбор многих исходных данных при проектировании, о чём дополнительно будет сказано в последующих лекциях. В то же время существует ещё один особенный элемент в теории насосов, без которого также невозможно реальное проектирование. Этим элементом является кавитация в насосах, а точнее способ её учёта при проектировании и эксплуатации. Именно этот элемент является предметом рассмотрения в следующей лекции.