Вязкость дисперсных систем
Важной характеристикой структурно-механических свойств является течение. Течение бывает ламинарным и турбулентным.
Ламинарное течение – движение жидкости в виде параллельных слоев, имеющих различную скорость и не смещающихся между собой. Возникает при низкой скорости течения и малом перепаде давления.
Турбулентное течение – течение, сопровождающееся вихреобразованием.
В соответствие с уравнением Ньютона сила сопротивления при течении F прямо пропорциональна градиенту скорости du и площади поверхности потока S:
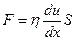- уравнение Ньютона
где η – коэффициент пропорциональости или вязкость, зависит от природы жидкости Единицей измерения вязкости является пуаз (пз), 1 пз = Па∙с= Н∙с/м2. Единица измерения вязкости названа в честь франц. учёного Пуазейля, который впервые изучал движение жидкости в капиллярах.
Ламинарное течение по трубкам или скорость течения жидкости из капилляра описывается уравнением Пуазейля (1842г.), которое было найдено экспериментальным путём:
,
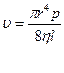где u - объемная скорость течения;
r – радиус капилляра трубки;
Δp – перепад давления или разность давления на обоих концах трубки;
Η – вязкость жидкости;
l – длина капилляра.
Величина, обратная вязкости 
называется текучестью – характеризует подвижность жидкости под влиянием внешних воздействий.
Жидкости, у которых отсутствует зависимость вязкости от характера взаимодействия частиц, подчиняются законам Ньютона и Пуазейля и называются ньютонскими жидкостями. Уравнение Ньютона и Пуазейля соблюдается, если жидкость движется ламинарно.
Вязкость дисперсных систем всегда превышает вязкость чистой дисперсионной среды. Зависимость вязкости коллоидной системы от концентрации дисперсной фазы выражается уравнением Эйнштейна (1906г.):
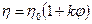- уравнение Эйнштейна,
где η – вязкость коллоидной системы;
η0 – вязкость чистого растворителя (дисперсионной среды);
φ – объемная доля частиц дисперсной фазы;
k – коэффициент, характеризующий форму частицы. Для сферической формы k = 2,5.
Для структурированных систем законы Ньютона не выполняются.
Дата добавления: 2015-08-11; просмотров: 4703;