Седиментация
Седиментация – это свободное оседание частиц в вязкой среде под действием гравитационного поля.
Для сферических частиц при их падении сила трения Fтр в жидкости равна: Fтр= 6 πηrU, где r – радиус частиц, η – вязкость среды, U – скорость оседания частиц.
Эффективный вес этих частиц будет равен G = 
π r3 (d - ρ)g, где d – плотность частиц дисперсной фазы, ρ – плотность среды, g- ускорение силы тяжести.
Постоянная скорость оседания достигается при равенстве силы трения и эффективного веса, тогда
.
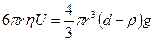Из этого уравнения скорость оседания равна
- закон Стокса
Закон Стокса был сформулирован в 1880 г. Из него следует два условия поведения частиц:
- если частица легче жидкости (например, эмульсия масла в воде), тогда d-ρ<0, => U<0 – условие всплывания частиц;
- если d- ρ>0, => U >0 – условие оседания частиц.
Зависимость скорости оседания на один сантиметр от радиуса частиц:
| диаметр частицы | время оседания |
| 200 мкм | 0,05 с |
| 2 мкм | 500 с |
| 20 нм | 58 дней |
Процессы седиментации противодействует диффузия частиц. Процесс диффузии проявляется сильнее с уменьшением радиуса частицы. Поэтому если процесс агрегации частиц не происходит, то только размер частиц определяет, будет ли седиментация.
Способность дисперсной системы сохранять равномерное распределение частиц по всему объему называется седиментационная устойчивость или кинетическая устойчивость.
Влияние на кинетическую устойчивость дисперсной системы диффузии или седиментации рассмотрим через сравнение диффузионного и седиментационного потока.
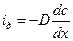
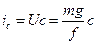
где U – скорость седиментации;
с – концентрация;
m – эффективная масса частицы;
g – ускорение силы тяжести;
f – коэффициент трения между коллоидной частицей и дисперсной средой.
,
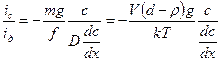где V – объём частицы, d – плотность дисперсной фазы, ρ – плотность дисперсионной среды.
Если iс/iд>>1, то на кинетическую устойчивость влияет только седиментация;
если iс/iд<<1 – только диффузия;
если iс/iд ≈ 1, => iс ≈ iд – необходимо учитывать оба процесса, устанавливается определённое распределение дисперсной фазы по высоте;
если iс = iд - наступает диффузионно-седиментационное равновесие, т.к. оно наступает при определенном градиенте концентрации, то в системе должно устанавливаться соответствующее распределение дисперсной фазы по высоте.
Определим закон этого распределения 
: учитывая что градиент концентрации изменяется по высоте, то заменив x на h, получим
=> 
.
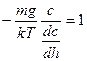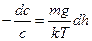При интегрировании от с0 до сh и от 0 до h получаем:
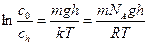или 
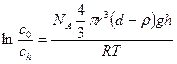- гипсометрический закон Лапласа-Перрена
(от лат. hypsos – высота)
тогда 
или 
, => 
.
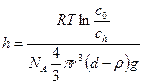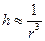Гипсометрический закон выполняется только для монодисперсных частиц. Значение высоты h резко падает с увеличением массы и размеров частиц.
Т.к. давление пропорционально концентрации: p=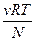 
, то это уравнение превращается в 
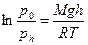- барометрический закон Лапласа
где М – молекулярный вес. Чем больше высота, тем больше давление.
Если частица имеет коллоидные размеры 1-10нм, путь, проходящий за счет броуновского движения намного больше, чем за счет силы тяжести. iд>iс – система седиментационно устойчива и подчиняется гипсометрическому закону Лапласа – Перрена.
Если система грубодисперсная, то сила тяжести преобладает, что значит - система не устойчива. iс/iд >> 1.
Если система частиц граничит по размеру с коллоидной, то путь в броуновском движении соизмерим с путем за счет силы тяжести: iс/iд ≈ 1. Такие системы разрушаются под действием силы тяжести, но поддаются седиментационному анализу.
Дата добавления: 2015-08-11; просмотров: 4218;