Диффузия
Вследствие молекулярно-кинетического движения частицы испытывают случайные смещения, при которых перемещаются вверх или вниз.
Диффузия – самопроизвольно протекающий в системе процесс выравнивания концентраций молекул, ионов или коллоидных частиц под влиянием их хаотического теплового движения.
В термодинамическом отношении процесс диффузии идёт с увеличением энтропии и является самопроизвольным. Явление диффузии необратимо и протекает до полного выравнивания концентраций.
Скорость диффузии при постоянных температуре и вязкости среды (t=const и η=const) зависит только от величины и формы частиц.
Медленность диффузии является признаком, отличающим коллоидные системы от истинных растворов низкомолекулярных веществ.
Перенос массы в результате диффузии формально сходен с законом переноса тепла и электричества. Воспользовавшись этой аналогией, Фик сформулировал (1855г.) первый закон диффузии:
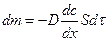- I закон Фика - стационарная диффузия
где m - количество продиффундировавшего вещества (моль);
D – коэффициент диффузии, зависит от свойств диффундирующих частиц и среды (м2/с);
dc/dx - градиент концентрации (моль/л);
S – площадь, через которую идет диффузия;
τ – продолжительность диффузии;
«-» так как диффузионный поток проходит в направлении меньших концентраций.
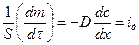- диффузионный поток
где iд –диффузионный поток, характеризует количество вещества, переносимое в результате диффузии за единицу времени через сечение, равное единице площади.
Принимая dс/dx =1, и S=1, τ=1, тогда получим
D = -m,
т.е. коэффициент диффузии (D) численно равен количеству вещества продиффундировавшего через единицу площади за единицу времени, при градиенте концентрации равном единице.
А. Эйнштейн, изучая броуновское движение, установил связь коэффициента диффузии D со средним сдвигом 
:
= 2Dt – закон Эйнштейна-Смолуховского
что дает возможность экспериментально установить коэффициент диффузии по методу сдвига.
Рассматривая силы трения, действующую со стороны растворителя на диффузию молекул растворенного вещества, Эйнштейн предложил:
,
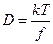где f – коэффициент трения для растворённых молекул (Нс/м); k – постоянная Больцмана.
С другой стороны, частица со стороны растворителя испытывает силу трения или сопротивление, равное
f= 6 πηr – закон Стокса,
где η – вязкость растворителя, r – радиус частицы.
Отсюда получим:
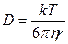или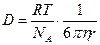 
– уравнение Эйнштейна-Стокса
для сферических частиц.
Это уравнение – одно из уравнений коллоидной химии, позволяет определить размер частиц:
,
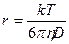отсюда молекулярный вес: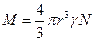 
, где γ- плотность дисперсной фазы, N – количество частиц.
Уравнение Эйнштейна-Стокса выражает физический смысл коэффициента диффузии. Величина kT – мера тепловой или кинетической энергии молекулы, η – мера вязкого сопротивления диффузии. Отношение kT и η определяет насколько легко частица диффундирует. Из уравнения Эйнштейна-Стокса следует, что D обратно пропорционально радиусу,
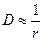
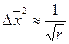
Осмотическое давление коллоидных систем
Рис. 26. Схема, поясняющая понятие осмотического давления.
Перегородка – непроницаемая мембрана для коллоидных частиц (рис. 26). Наличие мембраны ограничивает свободное движение коллоидных частиц в сторону чистой жидкости. Различие в концентрации раствора по обе стороны мембраны не может выровняться путём свободной диффузии. Растворитель переходит в раствор до тех пор, пока этот переход не компенсируется встречно направленным гидростатическим давлением со стороны раствора, это и есть осмотическое давление раствора π.
Осмотическое давление увеличивается из-за перехода части растворителя в сравнении с первоначальным.
Осмотическое давление для разбавленных коллоидных растворов находиться из уравнения:
,
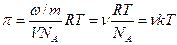где ω – количество растворенного вещества;
m – масса частицы;
NA – число Авогадро;
V – объем системы;
Т – температура;
ν - частичная концентрация.
Это уравнение аналогично уравнению Вант-Гоффа для осмотического давления истинных растворов:
,
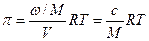где М – молекулярный вес; с – весовая концентрация.
Осмотическое давление для лиозолей очень маленькая величина и непостоянная, т.к. большие количественные различия в значениях концентрации приводят к слабому проявлению осмоса.
Определим количественную зависимость осмотического давления π от числа частиц n среднего радиуса r и степенью дисперсности z в единице объёма: имеем две дисперсные системы с одинаковым растворителем, при одинаковой температуре масса диспергированного вещества в этих системах выражается:
=> 
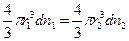
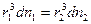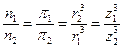
т.е. осмотическое давление обратно пропорционально кубу радиуса частиц и, следовательно, прямо пропорционально кубу степени дисперсности.
Значит небольшое изменение в размере частиц приведёт к значительному изменению осмотического давления.
Дата добавления: 2015-08-11; просмотров: 3099;