Средства обеспечения дисциплины 9 страница. За счет кинетической энергии вращения тело может совершать работу

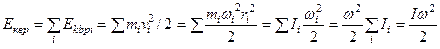
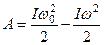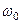За счет кинетической энергии вращения тело может совершать работу. Эта работа должна равняться изменению кинетической энергии вращения , где и 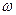– начальная и конечная угловые скорости вращения. Кинетическая энергия вращающихся тел используется в технике, например, при внезапном увеличении нагрузки машина не останавливается, а совершает работу за счет запаса кинетической энергии вращения маховика.

Найдем работу, совершаемую внешней силой при вращении твердого тела. Рассмотрим частный случай, когда сила направлена по касательной к окружности, по которой движется точка приложения силы (рис. 7.12). В этом случае сила 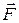и перемещение 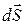точки ее приложения коллинеарны. Элементарная работа

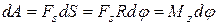(7.32)

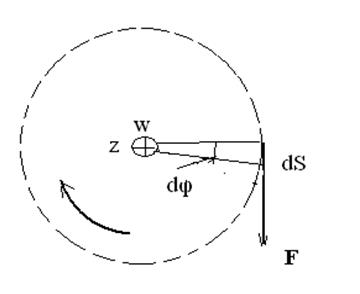
Рис.7.12

Поскольку направления оси 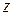и вектора 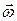совпадают, формулу (7.32) можно представить в виде

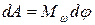, (7.33)

где 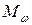– проекция вектора 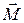на направление вектора .

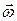13. Кинетическая энергия тела при плоском движении

Представим плоское движение тела как наложение поступательного движения со скоростью 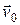некоторой точки О и вращения вокруг оси, проходящей через эту точку, с угловой скоростью 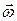. В этом случае скорость i-ой элементарной массы тела определяется формулой

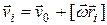, (7.34)

где 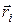– радиус-вектор i-ой массы, проведенной из точки О (рис. 7.13).

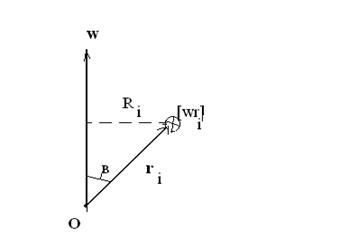
Рис. 7.13

Кинетическая энергия i-ой элементарной массы равна

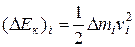(7.35)

Возведение в квадрат (7.34) с учетом (7.35) дает

.

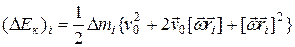Просуммировав по всем элементарным массам, найдем кинетическую энергию тела: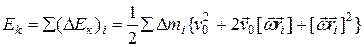

Разобьем полученное выражение на три слагаемых, вынося при этом постоянные множители за знак суммы:

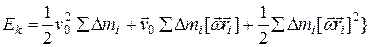(7.36)

Сумма элементарных масс даст массу тела 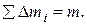Следовательно, первое слагаемое равно .

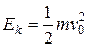Третье слагаемое в (7.36) равно 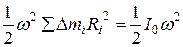, где 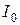– момент инерции тела относительно оси вращения О.

Второе слагаемое можно представить в ви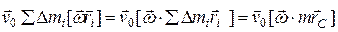де , где 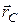– радиус-вектор, центра масс, проведенный из точки О.С учетом сказанного можно написать, что

В первое слагаемое входят только величины, характеризующие поступательное движение, в третье – только величины, характеризующие вращательное движение. Второе же слагаемое содержит величины, характеризующие как поступательное, так и вращательное движение.

Если в качестве точки О взять центр масс тела С, то 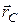будет равен нулю и последняя формула упростится: 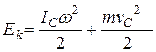, где 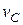– скорость центра масс, 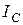– момент инерции тела относительно оси, проходящей через центр масс.

Таким образом, если разбить плоское движение тела на поступательное со скоростью центра масс и вращение вокруг оси, проходящей через центр масс, то кинетическая энергия распадается на два независимых слагаемых, одно из которых определяется только величинами, характеризующими поступательное движение, а другое – только величинами, характеризующими вращение.

14. Свободные оси вращения

Существуют такие оси вращения тел, которые не изменяют своей ориентации вращения в пространстве без действия на нее внешних сил. Эти оси называются свободными осями вращения (или осями свободного вращения). Можно показать, что в любом теле существуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями. Они называютсяглавными осями инерции тела.Например, главные оси инерции однородного прямоугольного параллелепипеда проходят через центры противоположных граней (рис. 7.14).

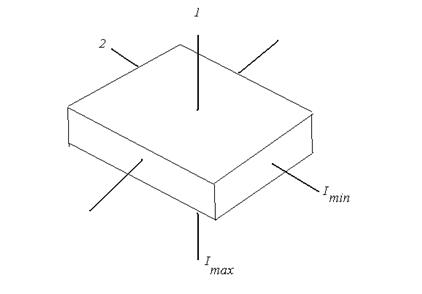
Рис. 7.14

Для однородного цилиндра одной из главных осей инерции является его геометрическая ось, а в качестве остальных осей могут быть две любые взаимно перпендикулярные оси, проведенные через центр масс в плоскости, перпендикулярной геометрической оси цилиндра. Главными осями инерции шара являются любые три взаимно перпендикулярные оси, проходящие через центр масс.

Для устойчивости вращения большое значение имеет, какая именно из свободных осей служит осью вращения.

Вращение вокруг главных осей с наибольшим и наименьшим моментами инерции оказывается устойчивым, а вращение около осей со средним моментом – неустойчивым. Так, если тело, имеющее форму параллелепипеда, подбросить, одновременно приведя его во вращение, то он, падая, будет устойчиво вращаться вокруг осей 1 и 2.

15. Гироскоп

Свойство свободных осей сохранять свое положение в пространстве широко применяется в технике, наиболее интересны в этом плане гироскопы.

Гироскопом (или волчком) называется массивное симметричное тело, вращающееся с большой скоростью вокруг оси симметрии. У симметричного тела направления момента импульса 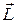и угловой скорости 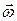совпадают, поэтому 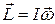. Вследствие массивности гироскопа его момент инерции очень велик, велика также угловая скорость.

Рассмотрим гироскоп, ось которого закреплена одним концом в шарнире О, вокруг которого она может поворачиваться без трения произвольным образом (рис. 7.15).

Рис.7.15. Ось гироскопа ОА, ось ВВ и сила F лежат в плоскости чертежа. Векторы Ми 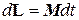направлены за чертеж. Ось DD перпендикулярна к плоскости чертежа

Попытаемся повернуть ось гироскопа ОА вокруг оси DD, подействовав на свободный конец оси силой F в течение времени dt. Однако гироскоп «проявит непослушание» – его ось повернется не вокруг оси DD, а вокруг оси ВВ, приняв положение ОА'. Это, казалось бы, противоестественное поведение гироскопа называют гироскопическим эффектом.

Гироскопический эффект находится в полном согласии с законами механики твердого тела. Действительно, согласно уравнению изменения момента импульса со временем в результате действия силы Fв течение времени dt момент импульса Lполучит приращение 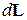. Обозначим через М – момент силы Fотносительно точки О. Тогда изменение момента импульса равно 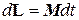. Новое значение момента импульса, равно 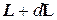. Оноокажется повернутым вокруг оси ВВ относительно первоначального значения L. Поскольку вектор Lнаправлен вдоль оси гироскопа, вместе с Lповернется и ось, перейдя из положения О А в положение О А'.

Гироскопический эффект является причиной того, что хорошо раскрученный детский волчок не опрокидывается под действием силы тяжести. Это действие приводит лишь к тому, что ось волчка поворачивается, описывая конус. Такое движение оси называется прецессией.

Рассмотрим простейший вид прецессии, называемый регулярной прецессией. Пусть один из концов оси гироскопа закреплен в шаровом шарнире О, позволяющем ей свободно поворачиваться в любом направлении (рис. 7.15). На гироскоп действует сила тяжести, которая лежит в вертикальной плоскости ОАО'. Обозначим через т – массу гироскопа вместе с осью. Момент силы Мперпендикулярен к этой плоскости. Пусть b – расстояние от шарнира О до центра масс гироскопа С, 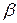– угол, образованный осью гироскопа с вертикалью. Тогда плечо силы 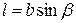. За время dt момент импульса получает приращение 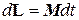, в результате чего вертикальная плоскость, в которой лежат ось гироскопа и сила тяжести mg, поворачивается на угол 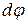. Вместе с ней поворачивается и вектор 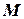. Расстояние О'А численно равно .

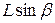Таким образом, на гироскоп действует опрокидывающий момент 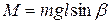. Будем откладывать вектор момента импульса гироскопа Lиз точки О. В момент времени t вектор Lизображается отрезком ОА. За время dt вектор Lполучит перпендикулярное к нему приращение 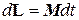,в результате чего он, оставаясь постоянным по модулю и не изменяя угла 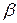с вертикалью, переходит в положение ОВ. В новом положении имеет место такое же взаимное расположение векторов L и М, какое было в момент t. Поэтому за последующий элемент времени dt вертикальная плоскость, в которой лежит ось гироскопа, снова повернется на угол 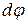и т.д. В итоге ось гироскопа будет поворачиваться вокруг вертикальной оси, описывая конус с углом раствора 2 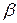. При этом вектор L будет изменяться только по направлению, оставаясь неизменным по модулю. Это объясняется тем, что элементарные приращения 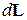все время будут перпендикулярными вектору L. Аналогично ведет себя вектор скорости при равномерном движении частицы по окружности. Вектор vполучает за время dt перпендикулярное к нему приращени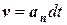е , где 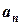– постоянное по модулю нормальное ускорение. В результате изменяется только направление вектора 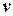, модуль же его остается постоянным.

Рис. 7.16.

Таким образом, в поле сил тяжести ось гироскопа с неподвижной точкой поворачивается вокруг вертикали, описывая конус. В случае, когда 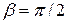, конус вырождается в плоскость. Такое движение гироскопа называется регулярной прецессией. Угловую скорость прецессии 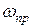можно найти, разделив угол 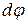на соответствующее время dt. Из рис. 7.16 следует, что .

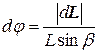Из соотношения 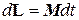вытекает, что 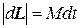. Поэтому .

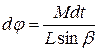Отсюда, с учетом того, что 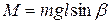, a 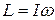получаем формулу

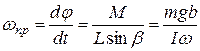(7.37)

Здесь I – момент инерции вращающихся частей гироскопа, 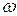– угловая скорость вращения гироскопа вокруг своей оси, 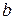– расстояние oт центра масс гироскопа.

Из формулы (7.37) видно, что угловая скорость прецессии не зависит от угла 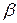, образованного осью гироскопа с направлением вверх по вертикали (этот угол может иметь значения от 0 до ).

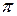Нужно иметь в виду, что формула (7.37) справедлива только при условии, что

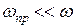(7.38)

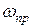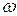Действительно, прецессирующий гироскоп участвует одновременно в двух вращениях, совершающихся со скоростью и . Поэтому его момент импульса определяется выражением, более сложным, чем 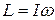. Только при соблюдении условия (7.38) можно полагать, что .

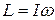Из формулы (7.37) следует, что условие (7.38) эквивалентно условию 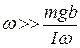, т.е. .

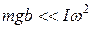Выражение mgb по порядку величины равно потенциальной энергии гироскопа Е_р. Выражение 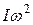по порядкуесть кинетическая энергия гироскопа Е_к.. Поэтому условие справедливости формулы (7.37) можно представить в виде ^.

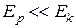Вычислим полную механическую энергию гироскопа. За нуль примем значение потенциальной энергии при 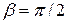. Будем считать, что 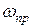можно пренебречь по сравнению с 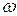. Тогда полная механическая энергия гироскопа определяется выражением .

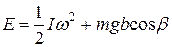В отсутствие трения полная энергия сохраняется, следовательно, 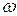также не уменьшается. Отсюда следует, что 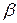= const. К этому результату мы уже пришли ранее.

16. Степени свободы и связи абсолютно твердого тела

Число независимых координат, однозначно определяющих положение тела в пространстве, называется степенью свободы. Ясно, что положение точки в пространстве можно характеризовать тремя прямоугольными координатами 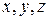. Вместо таких координат можно взять и полярные координаты. Но их будет не более трех. Поэтому говорят, что материальная точка обладает тремя степенями свободы.

Однако не всегда перемещение точки в заданных условиях будет каким угодно. Рассмотрим, например, маленький шарик, привязанный к концу нерастяжимой нити, другой конец которой закреплен. Если нить натянута, то шарик может перемещаться только по поверхности сферы с центром в точке закрепления. Можно привести и другие примеры, в которых материальная точка все время вынуждена находиться на какой-либо заданной поверхности. В таких случаях говорят, что на ее движение наложены связи. Координаты 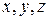такой точки должны соответствовать соотношению вида 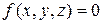, который является уравнением рассматриваемой поверхности. Ввиду этого остаются независимыми только две координаты. Третья координата может быть вычислена из уравнения связи 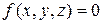. В этих случаях точка обладает двумя степенями свободы.

Пусть имеется механическая система, состоящая из произвольного числа 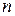материальных точек. Если эти точки движутся без всяких ограничений, то для мгновенного определения их положения надо задать 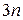координат. Следовательно, система имеет 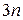степени свободы. Однако в некоторых случаях свобода перемещения точек ограничена. На 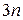координат налагаются дополнительные условия, называемые связями. Обозначим его 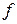. Следовательно, данная механическая система имеет 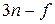степени свободы.

Определим число степеней свободы абсолютно твердого тела. Ясно, что для однозначного определения положения твердого тела достаточно задать положение каких-либо трех его координат А, В, С, не лежащих на одной прямой (рис.7.17).

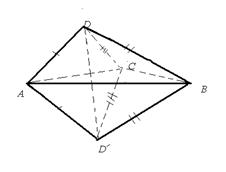
Рис.7.17

Возьмем четвертую точку D. Расстояния AD, BD и CD для рассматриваемого твердого тела известны. Кроме того, при любых движениях твердого тела точка D все время должна находиться по одну и ту же сторону плоскости треугольника ABC. Чтобы определить положение в пространстве точки D, построим по заданным длинам AC, AD, CD треугольник ADC. Чтобы найти положение точки D, будем вращать треугольник ADC вокруг основания AC, пока вершина D не окажется на заданном расстоянии от третьей точки B. Этому условию соответствуют две точки D и D^ґ. Но вторая точка не отвечает условию задачи, так как она находится не с той стороны от плоскости треугольника ABC. Таким образом, зная положения трех точек А, В, С, можно геометрическим построением найти положение любой другой точки твердого тела.

Положения трех точек А, В, С можно задать их прямоугольными координатами 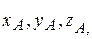, , 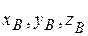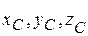. Эти девять координат не свободны, а связаны тремя соотношениями

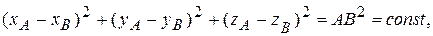
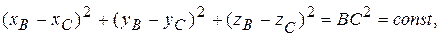
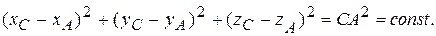
Независимыми остаются только шесть координат, поскольку длины AB, BC и СA не изменяются. Поэтому твердое тело имеет шесть степеней свободы.

При ограничении свободы движения число степеней свободы твердого тела уменьшается. Например, твердое тело, одна из точек которого неподвижно закреплена, может только вращаться вокруг этой неподвижной точки, и имеет три степени свободы. Твердое тело, которое может только вращаться вокруг закрепленной оси, имеет одну степень свободы. Если же твердое тело может скользить вдоль закрепленной оси и одновременно вращаться вокруг нее, то число степеней свободы становится равным двум.

17. Условия равновесия твердого тела. Виды равновесия

Как было указано в предыдущем разделе, твердое тело является механической системой с шестью степенями свободы. Для описания его движения требуется шесть независимых числовых уравнений. Вместо них можно взять два независимых векторных уравнения. Таковыми являются уравнение движения центра масс

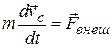(7.38)

и уравнение моментов

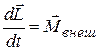(7.39)

Если твердое тело покоится, то уравнения (7.38) и (7.39) переходят в уравнения

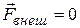(7.40)

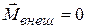(7.41)

В этих формулах 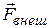– результирующая внешних сил, 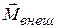– сумма моментов этих сил относительно оси вращения. Таким образом, равновесие имеет место в том случае, когда результирующая внешних сил и сумма моментов относительно оси вращения равны нулю.

Это – необходимые условия равновесия твердого тела. Но они не являются достаточными. При их выполнении центр масс может еще двигаться прямолинейно и равномерно с произвольной скоростью, а само тело может вращаться с сохранением вращательного импульса. Так как при равновесии 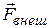равна нулю, то момент этих сил 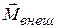в состоянии равновесия не зависит от положения неподвижного начала О, относительно которого он берется. Поэтому при решении любой задачи на равновесие твердого тела начало О можно выбирать произвольно.

Различают устойчивое и неустойчивое равновесия. Как показывает связь силы с потенциальной энергией, при равенстве нулю результирующих внешних сил в состоянии равновесиявсе производные потенциальной энергии по координатам должны обращаться в нуль. Отсюда следует, что для равновесия необходимо, чтобы потенциальная энергия была стационарна. Стационарность означает, что при всяком выводе системы из состояния равновесия, когда координаты материальных точек получают бесконечно малые приращения, функция потенциальной энергии остается почти постоянной. Точнее, приращения потенциальной функции при таких приращениях координат являются бесконечно малыми более высокого порядка, чем приращения самих координат. В частности, система будет находиться в равновесии, если потенциальная энергия экстремальна, т.е. минимальна или максимальна.

Если потенциальная энергия минимальна, то равновесие будет устойчивым. Диссипативные силы делают равновесие еще более устойчивым. Если потенциальная энергия максимальна, равновесие тела неустойчиво.

Эти выводы остаются справедливыми и для систем, свобода перемещения которых ограничена наложенными связями. Надо только потребовать, чтобы связи были идеальными, т.е. такими, которые не производят работы при любых возможных перемещениях системы. Примером может служить идеально гладкий шарик, надетый на идеально твердую и гладкую спицу, которая задает направление возможного перемещения шарика. Сила, действующая на шарик со стороны спицы, перпендикулярна направлению возможного перемещения и работы не производит.

18. Центр тяжести

На каждую точку частицы твердого тела действует сила тяготения Земли. Все силы тяготения параллельны друг другу, если размеры тела невелики относительно радиуса Земли, и имеют равнодействующую. Оказывается, как бы ни повернули твердое тело, эта равнодействующая будет проходить через одну точку, неизменно связанную с телом. Эта точка называется центром тяжести тела.

Если укрепить тело в точке центра тяжести, то оно будет находиться в равновесии при любом положении тела. Следовательно, сумма моментов сил тяжести всех частиц тела относительно любой горизонтальной оси, проходящей через центр тяжести, равна нулю. Подвешенное так тело после поворота вокруг любой оси, проходящей через центр тяжести, будет оставаться в равновесии, так как равнодействующая сил тяжести проходит через точку закрепления.

Центр масс твердого тела совпадает с его центром тяжести. Поэтому вместо терминов “центр масс” и “центр инерции” употребляют также термин “центр тяжести”. Следовательно, координаты центра тяжести можно найти по формуле, справедливой для радиуса-вектора центра масс, о которой мы говорили в разделе “Центр масс системы материальных точек”. Положение центра тяжести можно вычислить также по формулам (7.40) и (7.41).

Центр тяжести можно определить и экспериментально.

Контрольные вопросы

1. Что характерно для скоростей и ускорений точек тела, движущегося поступательно?

2. Чему равно ускорение центра масс тела, имеющего массу m и находящегося под действием сил 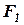и ?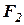

3. От каких величин зависит угловое ускорение тела?

4. Могут ли момент импульса и угловая скорость вращающегося тела быть неколлинеарными?

5. Приведите примеры проявления закона сохранения момента импульса твердого тела.

6. Что такое момент инерции тела?

7. Какова роль момента инерции тела во вращательном движении?

8. Выведите и сформулируйте уравнение динамики вращательного движения твердого тела.

9. Что такое момент импульса материальной точки? Твердого тела? Как определяется направление момента импульса?

10. В чем заключается физическая сущность закона сохранения момента импульса? В каких системах он выполняется? Приведите примеры.

11. Сопоставьте основные уравнения динамики поступательного и вращательного движений, прокомментировав их аналогии.

12. Что такое свободные оси (главные оси инерции)? Какие из них являются устойчивыми?

13. В каком случае кинетическая энергия вращающегося тела определяется формулой 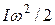? Как ее вывести?

14. Что называется моментом силы относительно неподвижной точки? Относительно неподвижной оси? Как определяется направление момента силы?