Средства обеспечения дисциплины 5 страница. Способы уменьшения сил трения.
Способы уменьшения сил трения.
1. Максимальная величина силы трения покоя заметно уменьшается или может совсем исчезнуть при наличии между поверхностями трущихся тел тонкого слоя вязкой жидкости (смазки). Сила, действующая на твердое тело, движущееся в жидкой среде, со стороны прилегающих к телу слоев жидкости вдоль поверхности тела, называется силой жидкого трения.Опыт показывает, что эта сила зависит от скорости тела 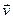 относительно среды. При малых скоростях она пропорциональна скорости и выражается формулой
относительно среды. При малых скоростях она пропорциональна скорости и выражается формулой
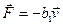 , (4.19)
, (4.19)
а по мере возрастания скорости сила жидкого трения растет пропорционально квадрату скорости:
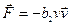 (4.20)
(4.20)
Коэффициенты 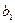 и
и 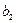 называются коэффициентами трения (или сопротивления). Они зависят от:
называются коэффициентами трения (или сопротивления). Они зависят от:
- свойств жидкости, в частности, вязкости и плотности; их величина возрастает с увеличением вязкости;
- формы и размеров тела; если тела имеют одинаковую геометрическую форму, они возрастают с увеличением наибольшей площади сечения тела в направлении, перпендикулярной скорости, и уменьшаются для тел с одинаковым сечением при приближении их формы к обтекаемой ”каплеобразной’’ форме.
2. Замена скольжения качением: применение колес, катков, шариковых и роликовых подшипников. Возникающая при этом сила трения называется силой трения качения.Она выражается формулой:
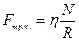 , (4.21)
, (4.21)
где R – радиус катящегося тела, 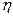 – коэффициент трения качения, зависящий от свойств материала соприкасающихся поверхностей и имеющая размерность длины; N – сила нормального давления (как и в предыдущих случаях).
– коэффициент трения качения, зависящий от свойств материала соприкасающихся поверхностей и имеющая размерность длины; N – сила нормального давления (как и в предыдущих случаях).
Семена некоторых растений (горох, каштан, орех) имеют шарообразную форму, поэтому они проявляют силы трения качения при откатывании на более далекие расстояния от материнского растения.
Контрольные вопросы
1. Какая система отсчета называется инерциальной? Почему система отсчета, связанная с Землей, строго говоря, неинерциальна?
2. В чем заключается физический смысл массы? Назовите её свойства.
3. Что такое сила? Как её можно охарактеризовать?
4. Является ли первый закон Ньютона следствием второго закона Ньютона? Почему?
5. Сформулировав три закона Ньютона, покажите, какова взаимосвязь между этими законами?
6. В чем заключается принцип независимости действия сил?
7. Назовите и охарактеризуйте виды взаимодействий.
8. Назовите особенности гравитационных сил?
9. Какова физическая сущность трения? В чем отличие сухого трения от жидкого?
10. Что называется механической системой? Какие системы называются замкнутыми? Является ли Вселенная замкнутой системой? Почему?
11. В чем заключается закон сохранения импульса? В каких системах он выполняется? Почему он является фундаментальным законом природы?
12. В чем измеряется коэффициент трения качения?
13. Какова роль силы трения в природе и технике? Ответ обоснуйте конкретными примерами.
14. В чем роль силы трения при качении тел?
15. Почему пассажиры любого вида транспорта при внезапной остановке наклоняются вперед, а при резком увеличении скорости движения – назад?
16. При каком условии пароход, плывущий против течения, будет иметь постоянную скорость?
17. Почему при выстреле пуля оставляет в стекле небольшое отверстие, а брошенная рукой – разбивает стекло на кусочки?
18. Канат переброшен через блок, причем часть каната лежит на столе, часть – на полу. После того как канат отпустили, он начал двигаться со временем равномерно. Определите скорость этого движения, если высота стола h.
19. Если концы деревянной палки положить на два стакана и с силой ударить палку тяжелым предметом посередине, палка переломится, а стаканы останутся целы. Как можно объяснить это явление?
20. Тело движется по горизонтальной поверхности. Форма траектории – окружность. Как будет изменяться вектор силы трения при движении?
21. Всегда ли трение скольжения больше трения качения?
22. Диаметр одного шарика в два раза больше, чем другого. После начального периода ускоренного движения шарики равномерно падают в воздухе. Плотность их одинакова. Сила сопротивления воздуха пропорциональна квадрату скорости и площади поперечного сечения шарика (площадь большого круга). Определите, во сколько раз различаются скорости падения шариков. Выталкивающей силой, действующей в воздухе на шарики, пренебречь.
23. На гладкую доску положили два кирпича, один плашмя, другой – на ребро. Вес кирпичей одинаков. Какой кирпич начнет сползать первым, если постепенно поднимать один конец доски?
24. Можно ли уничтожить трение между двумя поверхностями, тщательно их отшлифовав?
25. На спускающегося парашютиста действует сила земного притяжения, но движется он равномерно. Объясните это.
26. Масса одного тела меньше другого. Если бы Земля притягивала все тела с одинаковой силой, какое тело упало бы быстрее? Первоначально они находились на одинаковой высоте.
27. Шарику, который первоначально находился на горизонтальном столе высотой h, сообщили скорость v0, и он скатился по желобу на землю. Какую форму должен иметь желоб, чтобы при скатывании шарик все время касался желоба, не оказывая на него давления?
28. Какие часы целесообразно применять во время космических полетов: гиревые с маятником или пружинные? Как определить массу тела в мире невесомости?
29. Покажите, что второй закон Ньютона для тел, между которыми действуют гравитационные силы, не меняются при переходе от одной инерциальной системы отсчета к другой, движущейся со скоростью 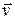 относительно первой.
относительно первой.
30. Зачем в вертолетах, кроме основного винта – ротора, создающего силу, направленную вверх, устанавливают на хвостовой балке небольшой винт, создающий тягу в направлении, приблизительно перпендикулярном к направлению полета?
31. Что является более прочным для удержания одного и того же веса – гамак или качели, находящиеся в покое?
32. Альпинисты переправляются через глубокий овраг, держась руками на натянутую над ними веревку. Что целесообразнее для безопасности – туго натянуть канат или ослабить его? В каком случае канат может скорее оборваться?
33. Как с помощью небольшой силы, имея трос, вытащить загрузший автомобиль?
34. В зависимости от угла наклона тело, находящееся на наклонной плоскости, может оставаться в покое, двигаться по ней равномерно или равноускоренно. Каково соотношение между действующими на тело силами во всех трех случаях?
35. Шнуром, перекинутым через блок, равномерно поднимают груз, натягивая конец шнура горизонтально. Чему равна сила давления на блок? Будет ли она больше (меньше) веса груза или равна ему?
36. Одно и то же тело взвесили на пружинных весах на экваторе и полюсе. Каковы показания приборов?
37. Почему скорость поезда на горизонтальном участке пути не возрастает бесконечно, если сила тяги двигателя действует непрерывно?
38. Тела падают вследствие притяжения Земли. В чем неточность этого выражения?
39. Как объяснить, что бегущий человек, споткнувшись, падает в направлении своего движения, а, поскользнувшись, падает в направлении, противоположном направлению своего движения?
40. Докажите свойство аддитивности массы. Верно ли утверждение о том, что аддитивность и закон сохранения массы вещества – одинаковые понятия?
Лекция №5. Динамика системы материальных точек
1. Центр масс системы материальных точек
На практике не каждое тело может быть представлено как материальная точка. Однако всегда можно ее разделить на достаточно малые части, каждую из которых можно считать материальной точкой.
Ещё чаще приходится иметь дело не с одним-двумя телами, а с системой тел, взаимодействующих между собой. Изучение движения такой системы – весьма сложная задача, так как в общем случае для описания движения системы нужно знать движение всех её частей. Такое изучение облегчается тем, что у самых различных систем имеются общие свойства. В частности, таким общим свойством является то, что в любой системе можно выделить особую по отношению ко всем другим точкам системы точку, которая называется центром масс системы.
Рассмотрим две материальные точки А и В с массами 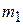 и
и 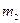 , расположенные в плоскости хОу.
, расположенные в плоскости хОу.
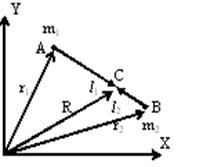 Рис. 5.1
Рис. 5.1
| Центром масс двух материальных точек А и В с массами 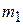 и и 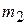 соответственно называется точка С, лежащая на отрезке, соединяющем А и В, на расстояниях соответственно называется точка С, лежащая на отрезке, соединяющем А и В, на расстояниях 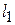 и и 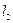 от А и В, (рис.5.1) обратно пропорциональных массам точек, т.е. от А и В, (рис.5.1) обратно пропорциональных массам точек, т.е.
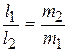 (5.1) (5.1)
|
При этом центр масс необязательно совпадает с какой-либо материальной точкой системы.
Если положения точек А и В задаются радиусами-векторами 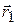 и
и 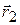 , то положение центра масс определяется радиусом-вектором
, то положение центра масс определяется радиусом-вектором 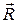 . Соединим массы
. Соединим массы 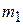 и
и 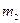 с центром массточек отрезками
с центром массточек отрезками 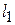 и
и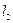 , направленными от точек А и В к центрумасс, как показано на рисунке. Тогда
, направленными от точек А и В к центрумасс, как показано на рисунке. Тогда
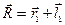 и
и 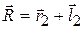 (5.2)
(5.2)
Умножим первое уравнение на 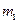 , а второе на
, а второе на 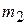 :
:
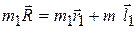 и
и 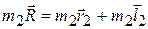
и сложим их: 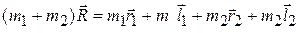 (5.3)
(5.3)
Но с учетом определения (5.1) и направлений векторов 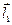 и
и 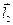 имеем, что
имеем, что 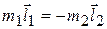 . Тогда из (5.3) получим соотношение:
. Тогда из (5.3) получим соотношение:
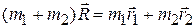 (5.4)
(5.4)
или 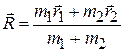 (5.5)
(5.5)
Формулы (5.4) и (5.5) могут быть обобщены на любое количество материальных точек. При этом радиус-вектор центра масс 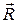 системы, состоящей из n материальных точек, определяется формулой
системы, состоящей из n материальных точек, определяется формулой
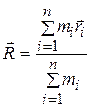 (5.6)
(5.6)
Здесь 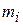 – масса точки с номером i,
– масса точки с номером i, 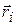 – её радиус-вектор, а
– её радиус-вектор, а 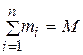 – полная масса системы точек.
– полная масса системы точек.
Из формулы (5.6) следуют формулы для вычисления координат центра масс через координаты и массы точек системы:
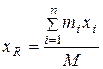 ,
, 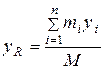 ,
, 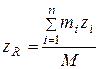 (5.7)
(5.7)
Скорость центра масс системы материальных точек также выражается через массы и скорости отдельных материальных точек системы. Действительно, в силу определения скорости запишем выражение для скорости центра масс в виде:
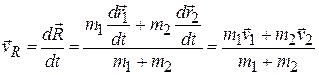 (5.8)
(5.8)
или
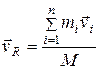 (5.9)
(5.9)
Так же может быть найдено и выражение для ускорения центра масс системы: 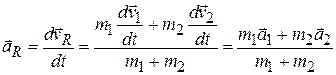 , т.е.
, т.е. 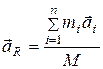 (5.10)
(5.10)
Величины 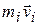 представляют собой импульсы отдельных точек, поэтому уравнение (5.9) можно переписать в виде:
представляют собой импульсы отдельных точек, поэтому уравнение (5.9) можно переписать в виде:
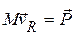 , (5.11)
, (5.11)
где 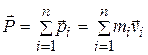 – импульс системы материальных точек. Таким образом, импульс системы материальных точек равен произведению массы системы на скорость её центра масс.
– импульс системы материальных точек. Таким образом, импульс системы материальных точек равен произведению массы системы на скорость её центра масс.
Дифференцируя (5.11), находим уравнение движения системы материальных точек в следующем виде:
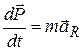 (5.12)
(5.12)
Отсюда следует, что центр масс системы движется как материальная точка, масса которой равна суммарной массе всей системы.
2. Закон сохранения импульса
Совокупность тел, выделенных для рассмотрения, называется механической системой. Тела системы могут взаимодействовать как между собой, так и с телами, не входящими в систему. В соответствии с этим силы, действующие на тела системы, подразделяются на внутренние и внешние. Внутренними называют силы, с которыми тела системы действуют друг на друга,а внешними – силы, действующие со стороны тел, не принадлежащих системе.Обозначим внутренние силы через 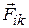 , где первый индекс указывает номер частицы, на которую действует сила, второй индекс – номер частицы, воздействием которой обусловлена эта сила. Символом
, где первый индекс указывает номер частицы, на которую действует сила, второй индекс – номер частицы, воздействием которой обусловлена эта сила. Символом 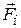 обозначим результирующую всех внешних сил, действующих на i-ую частицу. Согласно третьему закону Ньютона
обозначим результирующую всех внешних сил, действующих на i-ую частицу. Согласно третьему закону Ньютона 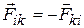 , т.е.
, т.е. 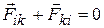 . Отсюда следует, что геометрическая сумма всех внутренних сил, действующих в системе, равна нулю.
. Отсюда следует, что геометрическая сумма всех внутренних сил, действующих в системе, равна нулю.
Рассмотрим движение механической системы, состоящей из двух материальных точек. Обозначим внутренние силы: через 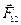 – силу, действующую на первую точку со стороны второй, и
– силу, действующую на первую точку со стороны второй, и 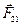 – силу, действующую на вторую точку со стороны первой. Сумму внешних сил, действующих на первую и вторую точки, обозначим через
– силу, действующую на вторую точку со стороны первой. Сумму внешних сил, действующих на первую и вторую точки, обозначим через 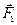 и
и 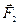 соответственно.
соответственно.
Движение каждой точки описывается вторым законом Ньютона:
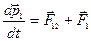 ,
, 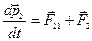 , (5.13)
, (5.13)
где 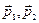 – импульсы точек с массами
– импульсы точек с массами 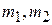 . Сложив эти два уравнения, получим:
. Сложив эти два уравнения, получим:
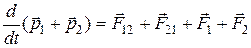 (5.14)
(5.14)
Согласно третьему закону Ньютона, внутренние силы попарно равны и противоположны, т.е. 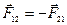 . Поэтому в формуле (5.14) сумма внутренних сил обращается в нуль. С другой стороны, по определению
. Поэтому в формуле (5.14) сумма внутренних сил обращается в нуль. С другой стороны, по определению 
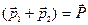 – импульс системы. Таким образом,
– импульс системы. Таким образом,
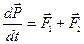 (5.15)
(5.15)
Легко видеть, что в случае произвольного числа n материальных точек в левой части всегда будет производная полного импульса системы, а в правой части – сумма всех внешних сил. Поэтому в общем случае имеем
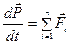 , (5.16)
, (5.16)
т.е. производная по времени импульса системы материальных точек равна сумме всех внешних сил, действующих на точки системы. Уравнение (5.16) называют законом изменения импульса системы материальных точек или теоремой о движении центра масс.
Согласно этой теореме центр масс движется как материальная точка, на которую действует сила, равная геометрической сумме всех внешних сил, действующих на систему. Примером может служить движение снаряда по параболе в безвоздушном пространстве. Если в какой-либо момент времени снаряд разорвется на мелкие осколки, то эти осколки под действием внутренних сил будут разлетаться в разные стороны.Однако центр масс осколков и газов, образовавшихся при взрыве, будет продолжать свое движение по параболической траектории, как если бы никакого взрыва не было.
Как видно из уравнения (5.16), изменение суммарного импульса определяется равнодействующей всех внешних сил, действующих на систему. В связи с этим рассмотрим ряд важных следствий, вытекающих из уравнения (5.16).
1. Рассмотрим систему материальных точек, которая не подвергается воздействию внешних сил.Такая система называется замкнутой.В этом случае правая часть уравнения (5.16) в любой момент времени равна нулю. Тогда
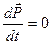 (5.17)
(5.17)
Это значит, что 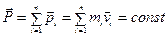 (5.18)
(5.18)
Уравнение (5.18) называется законом сохранения импульса: полный импульс всех тел замкнутой системы сохраняется во времени.
Можно также показать, что при выполнении условия (5.17) центр масс замкнутой системы движется равномерно и прямолинейно.
2.Внешние силы на точки системы действуют, но их сумма равна нулю. В этом случае также выполняется закон сохранения импульса. Например, если тела движутся по гладкой горизонтальной поверхности, то силы тяжести и силы реакции со стороны поверхности, действующие на эти тела и являющиеся внешними, все время равны и противоположны.
3.Так как уравнение (5.18) векторное, то оно выполняется также для проекций на любое направление. Поэтому, если сумма проекций внешних сил на какое-то направление в любой момент времени равна нулю, то проекция импульса системы на это направление остается постоянной, хотя проекции импульса на другие направления могут при этом изменяться.
Примерами действия закона сохранения импульса могут служить отдача при стрельбе из огнестрельного оружия, реактивное движение, перемещение осьминогов и т.п.
Закон сохранения импульса справедлив не только в классической механике, хотя он получен как следствие законов Ньютона. Эксперименты показывают, что он выполняется и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики). Этот закон носит универсальный характер, т.е. закон сохранения импульса – фундаментальный закон природы.
В природе реактивное движение используется некоторыми живыми организмами. Например, кальмары, спруты, медузы и некоторые двухстворчатые моллюски передвигаются посредством отдачи воды, выбрасываемой ими из особых полостей тела. При этом кальмары развивают большую скорость движения – 70 км/час.
Своеобразным примером реактивного движения является «бешеный огурец» – растение южного Крыма. Внутри созревшего плода этого растения находится жидкость под повышенным давлением. Оторванный от стебля «бешеный огурец» вырывается из рук и отлетает в сторону за счет отдачи струи жидкости, выбрасываемой из отверстия, образующегося в месте крепления к плодоножке.
3. Движение тел с переменной массой. Реактивное движение
Выведем уравнение движения материальной точки с переменной массой на примере движения ракеты. Принцип действия ракеты заключается в следующем. Ракета с большой скоростью выбрасывает вещество (газы), воздействуя на него с огромной силой. Выбрасываемое вещество той же силой, но противоположно направленной, в свою очередь действует на ракету и сообщает ей ускорение в противоположном направлении. Если нет внешних сил, то ракета вместе с выброшенным веществом является замкнутой системой. Импульс такой системы не может меняться во времени.
Пусть 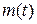 – масса ракеты в произвольный момент времени
– масса ракеты в произвольный момент времени 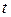 , а
, а 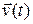 – ее скорость в тот же момент. Количество движения ракеты в этот момент времени будет
– ее скорость в тот же момент. Количество движения ракеты в этот момент времени будет 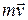 . Спустя время
. Спустя время 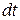 масса и скорость ракеты получат приращения. Заметим, что величина
масса и скорость ракеты получат приращения. Заметим, что величина 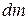 отрицательна. Количество движения ракеты станет равным
отрицательна. Количество движения ракеты станет равным 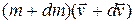 .
.
Обозначим через 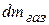 массу газов, образовавшихся за время
массу газов, образовавшихся за время 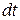 , а через
, а через 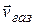 – их скорость. Тогда количество движения газов, образовавшихся за время
– их скорость. Тогда количество движения газов, образовавшихся за время 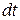 равно
равно 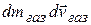 . Из современной формулировки второго закона Ньютона имеем, что
. Из современной формулировки второго закона Ньютона имеем, что
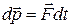 ,
,
где 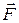 – геометрическая сумма всех внешних сил, действующих на ракету.
– геометрическая сумма всех внешних сил, действующих на ракету.
Таким образом,
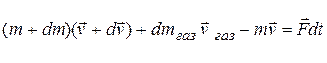 (5.19)
(5.19)
Раскрывая скобки и учитывая, что 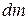 и
и 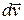 – малые величины за время
– малые величины за время 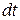 , можно отбросить произведение
, можно отбросить произведение 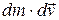 как бесконечно малую высшего порядка. Обозначим через
как бесконечно малую высшего порядка. Обозначим через 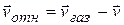 скорость истечения газов относительно ракеты, которую называют скоростью газовой струи ракеты.Кроме того, из закона сохранения массы следует, что
скорость истечения газов относительно ракеты, которую называют скоростью газовой струи ракеты.Кроме того, из закона сохранения массы следует, что
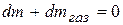 .
.
С учетом этих замечаний выражение (5.19) преобразуется к виду
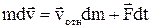 . (5.20)
. (5.20)
Разделим это выражение на 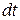 и из (5.20) получим
и из (5.20) получим
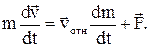 (5.21)
(5.21)
По форме уравнение (5.21) совпадает с уравнением, выражающим второй закон Ньютона. Однако масса тела 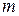 здесь не постоянна, а меняется во времени из-за потери вещества. Кроме того, в правой части выражение
здесь не постоянна, а меняется во времени из-за потери вещества. Кроме того, в правой части выражение 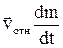 имеет смысл дополнительной внешней силы. Она называется реактивной силойи имеет значение силы, с которой действуют на ракету вытекающие из нее газы. Уравнение (5.21) впервые было получено русским механиком И.В.Мещерским и называется уравнением Мещерского или уравнением движения точки с переменной массой.
имеет смысл дополнительной внешней силы. Она называется реактивной силойи имеет значение силы, с которой действуют на ракету вытекающие из нее газы. Уравнение (5.21) впервые было получено русским механиком И.В.Мещерским и называется уравнением Мещерского или уравнением движения точки с переменной массой.
Применим уравнение(5.21) к движению ракеты, на которую не действуют никакие внешние силы. Полагая 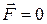 , получим
, получим
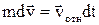 (5.22)
(5.22)
Предположим, что ракета движется прямолинейно в направлении, противоположном скорости газовой струи 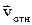 . За положительное направление примем направление полета. Тогда в скалярной форме уравнение (5.22) примет вид
. За положительное направление примем направление полета. Тогда в скалярной форме уравнение (5.22) примет вид
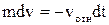 .
.
Следовательно,
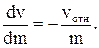 (5.23)
(5.23)
Скорость газовой струи может меняться во время полета. Однако для простоты мы примем, что она постоянна. В этом случае
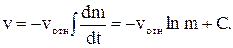
Значение постоянной интегрирования С определяется начальными условиями. Допустим, что в начальный момент времени скорость ракеты равна нулю, а ее масса равна 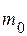 . Тогда предыдущее уравнение дает
. Тогда предыдущее уравнение дает
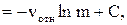 откуда
откуда 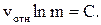
Следовательно,
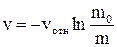 (5.24)
(5.24)
или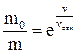 (5.25)
(5.25)
Формула (5.25) называется формулой Циолковского.
Формула Циолковского позволяет рассчитать запас топлива, необходимый для сообщения ракете определенной скорости. Она показывает, что:
- чем больше конечная масса ракеты, тем больше должна быть ее стартовая скорость;
- чем больше скорость истечения газов, тем больше может быть конечная масса при данной стартовой массе ракеты.
Уравнение Мещерского и формула Циолковского получены для нерелятивистских движений, т.е. для случаев, когда скорости 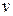 и
и 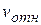 малы по сравнению со скоростью света.
малы по сравнению со скоростью света.
4. Задача двух тел. Приведенная масса
Рассмотрим замкнутую систему, состоящую из двух взаимодействующих материальных точек с массами 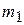 и
и 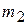 (рис.5.2). Уравнения движения этих точек можно записать в виде
(рис.5.2). Уравнения движения этих точек можно записать в виде
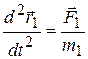 ,
,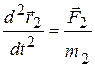 (5.30)
(5.30)
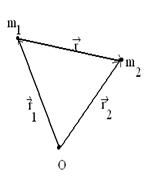
| Рис. 5.2. |
По третьему закону Ньютона 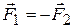 .
.
Вычитая из одного уравнения другое, находим
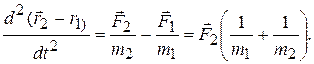
Это уравнение описывает движение одной материальной точки относительно другой, так как разность 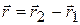 есть радиус-вектор, проведенный от первой точки ко второй. Он однозначно определяет положение второй точки относительно первой. Введем обозначение
есть радиус-вектор, проведенный от первой точки ко второй. Он однозначно определяет положение второй точки относительно первой. Введем обозначение
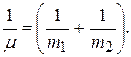 или
или 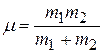 , (5.31)
, (5.31)
Дата добавления: 2015-08-11; просмотров: 1335;
