Средства обеспечения дисциплины 7 страница. Частица обладает моментом импульса независимо от формы траектории, по которой она движется

Частица обладает моментом импульса независимо от формы траектории, по которой она движется. Рассмотрим два частных случая.

1. Частица движется вдоль прямолинейной траектории (рис.6.4). Модуль момента импульса

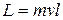(6.33)

может изменяться только за счет изменения модуля скорости.

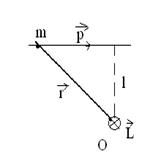
Рис.6.4

2. Частица движется по окружности радиуса 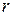(рис.6.5). Модуль момента импульса относительно центра окружности равен и так же, как и в предыдущем случае, может изменяться только за счет изменения модуля скорости. Несмотря на непрерывное изменение направления вектора 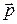, направление вектора 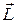остается постоянным.

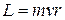(6.34)

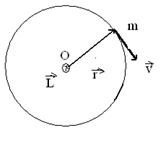
Рис. 6.5

9. Закон сохранения момента импульса

Выясним, от чего зависит изменение момента импульса частицы. С этой целью продифференцируем выражение (6.31) с учетом определения импульса частицы по времени: .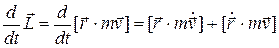

Согласно второму закону Ньютона 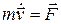– результирующая сил, действующих на частицу. По определению 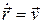. Поэтому можно написать, что .

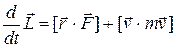Второе слагаемое является векторным произведением коллинеарных векторов и поэтому равно нулю. Первое слагаемое представляет собой момент силы относительно той же точки, относительно которой взят момент импульса. Следовательно, мы приходим к соотношению

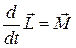(6.35)

Согласно уравнению (6.35) скорость изменения момента импульса со временем равна суммарному моменту сил, действующих на частицу.

Рассмотрим систему частиц, на которые действуют как внутренние, так и внешние силы. Моментом импульса 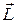системы относительно точки О называется сумма моментов импульса 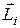отдельных частиц:

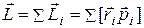(6.36)

Дифференцирование по времени дает, что

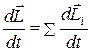(6.37)

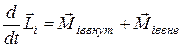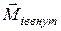В соответствии с (6.35) для каждой из частиц можно написать равенство , где – момент внутренних сил, а 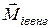– момент внешних сил, действующих на i-ую частицу. Подставим их в равенство (6.37), получим соотношение .

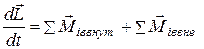Каждое из слагаемых в этих суммах представляет собой сумму моментов сил, действующих на i-ую частицу. Суммирование осуществляется по частицам. Если перейти к суммированию по отдельным силам, независимо от того, к какой из частиц они приложены, индекс I в суммах можно опустить.

Можно показать, что сумма моментов всех внутренних сил для любой системы частиц всегда равна нулю. Поэтому получаем, что

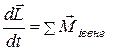(6.38)

Отсюда видно, что производная по времени от момента импульса системы равна сумме моментов внешних сил.

Если система замкнута, правая часть равенства (6.38) равна нулю и, следовательно, вектор 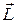не изменяется со временем. Отсюда вытекает закон сохранения момента импульса, который гласит, что момент импульса замкнутой системы материальных точек остается постоянным.

Момент импульса сохраняется и для незамкнутой системы материальных точек, если сумма моментов внешних сил равна нулю.

10. Законы сохранения и симметрия пространства и времени

Закон сохранения энергии является следствием однородности времени, закон сохранения импульса – следствием однородности пространства, а закон сохранения момента импульса – следствием изотропии пространства. Это означает, что перечисленные в нем законы сохранения можно получить из второго закона Ньютона, если к нему присоединить свойства симметрии пространства и времени, а именно: однородность пространства и времени, а также изотропию пространства.

Часто говорят, что однородность времени означает равноправие всех моментов времени. Однородность пространства означает, что в пространстве нет выделенных положений, все точки пространства равноправны. Аналогично, изотропия пространства характеризуется отсутствием в нем выделенных направлений, все направления в пространстве эквивалентны. Но такие формулировки слишком неопределенны и при буквальном понимании просто неверны. Направление к центру Земли, например, резко отличается от всякого горизонтального направления. Для альпиниста положения его у подножья и на вершине Эльбруса отнюдь не эквивалентны. Тело на вершине горы, представленное самому себе, может скатиться вниз. Но оно никогда не поднимется от подножья горы к ее вершине, если ему не сообщить надлежащей скорости. Точно так же для человека моменты времени, когда он молод, полон энергии и сил и когда он стар и находится на склоне лет, отнюдь не эквивалентны. Что же такое однородность времени, однородность и изотропия пространства?

Однородность времени означает, что если в два любые момента времени все тела замкнутой системы поставить в совершенно одинаковые условия, то, начиная с этих моментов, все явления в ней будут протекать совершенно одинаково.

Однородность пространства означает, что если замкнутую систему тел перенести из одного места пространства в другое, поставив при этом все тела в ней в те же условия, в каких они находились в прежнем положении, то это не отразится на ходе всех последующих явлений. В том же смысле надо понимать и изотропию пространства, только вместо переноса замкнутой системы надо говорить об ее повороте в пространстве на любой угол.

В связи с этими определениями отметим следующее: под замкнутой системой тел нельзя понимать всю Вселенную. Если поступить так, то перечисленные свойства симметрии пространства и времени стали бы самоочевидными. Но они стали бы и бессодержательными. Ибо говорить о переносе или повороте системы тел можно только по отношению к каким-то другим телам. Речь идет не о всей Вселенной в целом, а о таких ее частях, которые можно рассматривать как (приближенно) замкнутые системы. Отсюда ясно, что свойства симметрии пространства и времени, о которых мы говорили, отнюдь не самоочевидны. На них надо смотреть как на фундаментальные обобщения опытных фактов.

После этих разъяснений обратимся к выводу закона сохранения энергии в механике. Из динамики известно, что работа сил над механической системой равна приращению ее кинетической энергии, т.е.

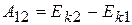(6.39)

Рассмотрим одну материальную точку, находящуюся под действием силы 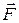. Предположим, что проекции силы 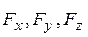могут быть получены дифференцированием потенциальной функции :

, ,

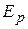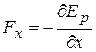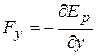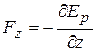
Однако сама потенциальная функция 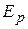может зависеть явно не только от координат 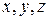рассматриваемой материальной точки, но и от времени t: 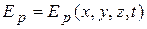. Например, это будет так, когда точка находится в силовом поле других тел, которое меняется во времени. Работа, производимая действующими силами над материальной точкой при перемещении ее вдоль некоторой кривой из положения 1 в положение 2, представляется интегралом 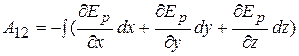, взятым вдоль той же кривой. Прибавим и вычтем под знаком интеграла член 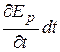. Тогда имеем

.

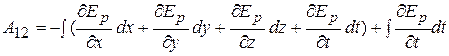Под первым интегралом находится полный дифференциал потенциальной функции 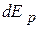. Поэтому

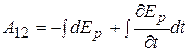(6.40)

В таком виде последнее равенство справедливо и для системы материальных точек. Поэтому дальнейшие рассуждения не связаны с предположением о том, что система состоит из одной материальной точки. После интегрирования (6.40) получаем

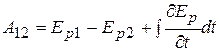(6.41)

Комбинация этой формулы с (6.38) приводит к соотношению

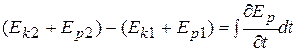(6.42)

До сих пор мы не использовали условие замкнутости системы и свойства однородности времени, поэтому наши рассуждения применимы и для незамкнутых систем. Допустим теперь, что система замкнута. Тогда ввиду однородности времени функция 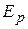не может явно зависеть от времени, т.е. .

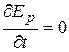В результате получим

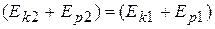, (6.43)

т.е. уравнение, выражающее закон сохранения механической энергии.

Докажем закон сохранения импульса. Допустим, что механическая система замкнута. Все силы 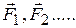, действующие на материальные точки системы, являются силами внутренними, внешних сил нет. Перенесем систему из произвольного положения 1 в другое произвольное положение 2, чтобы все материальные точки ее претерпели одно и то же перемещение 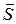и притом так, чтобы их скорости остались прежними по величине и направлению. Ввиду однородности пространства на такое перемещение не требуется затраты работы. Но эта работа представляется скалярным произведением 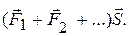Значит, она равно нулю, каково бы ни было перемещение. Отсюда следует, что для замкнутой системы 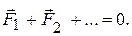А это есть как раз то условие, при выполнении которого из второго закона Ньютона получается закон сохранения импульса.

Закон сохранения момента импульса для замкнутой системы доказывается в точности так же. Используя изотропию пространства можно доказать, что геометрическая сумма моментов внутренних сил, действующих в системе, равна нулю: 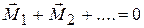. Отсюда немедленно следует рассматриваемый закон.

Контрольные вопросы

1. Что называется механической работой?

2. Как связаны между собой работа и энергия?

3. Напишите формулы для расчета работы постоянной и переменной силы?

4. Какую работу совершает равнодействующая всех сил, приложенных к телу, равномерно движущемуся по окружности?

5. Что называется мощностью? Выведите ее формулу.

6. Назовите единицы энергии, работы и мощности?

7. Какова связь между кинетической энергией материальной точки и работой приложенных к точке сил?

8. Как связана потенциальная энергия материальной точки с работой консервативных сил?

9. Работа силы, действующей на материальную точку, на любом пути равна нулю. Что можно сказать о взаимном направлении силы и скорости материальной точки?

10. Сила, действующая на материальную точку, изменяется по закону 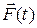, а скорость точки – по закону 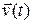. Чему равна мощность в момент ?

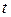11. Покажите, что если построить кривую, выражающую кинетическую энергию материальной точки как функцию пройденного пути, то сила, действующая в каждой точке в направлении перемещения, будет измеряться тангенсом угла наклона касательной в данной точке кривой энергии к оси абсцисс.

12. Являются ли силы трения консервативными?

13. Чем отличаются консервативные силы от неконсервативных?

14. В чем физический смысл потенциальной энергии?

15. Сформулируйте закон сохранения полной механической энергию. Назовите условия, при которых выполняется этот закон.

16. Какой удар называется центральным?

17. Чем отличается абсолютно упругий удар от абсолютно неупругого?

18. Определите скорости тел после абсолютно упругого и абсолютно неупругого ударов.

19. Два шара одинаковой массы сталкиваются, причем удар абсолютно упругий, но не центральный. Докажите, что в этом случае угол между направлениями скоростей шаров после удара равен 90⁰?

20. Шар массой 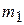налетает со скоростью 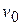на неподвижный шар массой 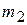, причем 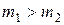. Удар абсолютно упругий, но не центральный. На какой максимальный угол может отклониться ударяющий шар?

21. Шар массой 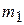налетает со скоростью 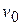на неподвижный шар массой 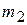. Удар абсолютно упругий и центральный. Скорости шаров после удара соответственно равны и 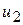. Каким соотношениям масс соответствуют следующие значения скорости: 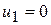, >0, <0?

22. Что называют моментом силы относительно произвольной точки?

23. Как найти направление вектора момента силы?

24. Докажите, что момент 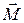не изменится, если точку приложения силы перенести в любую другую точку, расположенную на линии действия силы.

25. Что называется плечом силы?

26. Что называют моментом импульса?

27. Как найти направление вектора момента импульса?

28. Что называется плечом импульса?

29. Может ли обладать моментом импульса материальная точка, движущаяся по прямолинейной траектории?

30. Стоящий на полу пылесос при включении поворачивается в первый момент на небольшой угол. Почему это происходит?

31. Что такое однородность времени, однородность и изотропия пространства?

32. Какие дополнительные ограничения накладывает на вид потенциальной энергии изотропия пространства?

33. Выведите закон сохранения энергии, используя свойства однородности времени.

34. Выведите закон сохранения импульса, используя свойства однородности пространства.

35. Выведите закон сохранения момента импульса, используя свойства изотропии пространства.

Лекция №7. Механика твердого тела

1. Понятие об абсолютно твердом теле

Под абсолютно твердым телом в механике понимают тело, расстояния между любыми двумя материальными точками которого неизменны. Иначе говоря, форма и размеры его не изменяются, каковы бы ни были действующие на это тело силы. Здесь, как и вообще в классической механике, под материальными точками понимают не атомы или молекулы, а достаточно малые макроскопические части, на которые мысленно можно разделить рассматриваемую механическую систему. Естественно, такое представление об абсолютно твердом теле является абстракцией, применимой к тем случаям движения реальных тел, когда изменение формы и размеров этих тел под действием сил пренебрежимо мало. Допустима или нет такая, как и всякая другая идеализация – это определяется не только свойствами реальных тел, но и содержанием тех вопросов, на которые надо получить ответ. В дальнейшем для краткости вместо «абсолютно твердого тела» мы будем говорить только «твердое тело».

2. Твердое тело как система материальных точек

Разбив тело на элементарные массы 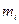можно представить его как систему материальных точек, взаимное расположение которых остается неизменным. Любая из этих элементарных масс может находиться под воздействием как внутренних сил, обусловленных её взаимодействием с другими элементарными массами рассматриваемого тела, так и внешних сил. Например, если тело находится в поле сил земного тяготения, на каждую массу тела 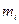будет действовать внешняя сила равная 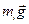. Однако сумма всех внутренних сил, действующих в системе, равна нулю.

Ранее было показано, что система материальных точек может характеризоваться центром масс системы, координаты которого определяются радиусом-вектором

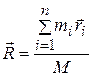(7.1)

Здесь 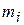– масса точки с номером i, 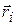– радиус-вектор, определяющий положение этой массы, а 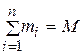– полная масса системы точек.

Выражение (7.1) не является вполне однозначным, поскольку каждый из векторов 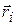можно проводить в любую из точек 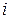-й элементарной массы. Чтобы устранить эту неопределенность, нужно взять предел выражения (7.1) при условии, что все из 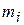стремятся к нулю: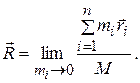

Таким образом, 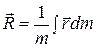, (7.2)

где интегрирование производится по всему телу.

Выражение (7.2) зависит от распределения массы по объему тела. Это распределение характеризуется плотностью вещества 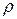. Для неоднородного тела плотность в точке Р определяется выражением

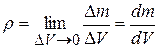, (7.3)

где 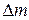– масса, заключенная в объеме 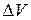, который включает в себя и точку Р. В формуле (7.3) уменьшение 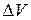до нуля не означает превращение его в точку. Под 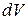подразумевается физически бесконечно малый объем, т.е. такой объем, который, с одной стороны, достаточно мал для того, чтобы макроскопические свойства (т.е. присущие большой совокупности атомов) вещества можно было считать в его пределах одинаковыми, а с другой стороны, достаточно велик, чтобы не могла проявиться дискретность (прерывистость) вещества.

Учитывая (7.3), формула (7.2) принимает вид

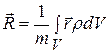, (7.4)

где интегрирование осуществляется по всему объему тела.

Если тело однородно, плотность во всех точках тела одинакова и ее можно вынести за знак интеграла в (7.4). Тогда

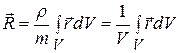(7.5)

Таким образом, в случае однородного тела радиус-вектор центра масс представляет собой значение радиус-вектора 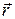, усредненное по всем точкам тела.

Итак, твердое тело эквивалентно системе материальных точек. Поэтому для него справедливо уравнение

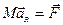, (7.6)

где 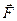– результирующая всех внешних сил, действующих на твердое тело.

Таким образом, центр масс твердого тела движется так, как двигалась бы материальная точка с массой, равной массе тела, под действием всех приложенных к нему сил.

Уравнение (7.6) дает возможность установить движение центра масс твердого тела, если известна масса тела и действующие на него силы.

3. Поступательное движение твердого тела

Простейший случай движения твердого тела – поступательное движение, т.е. такое движение, при котором все точки твердого тела движутся по подобным траекториям или любая прямая, связанная с телом, остается при его движении параллельной самой себе (рис. 7.1).

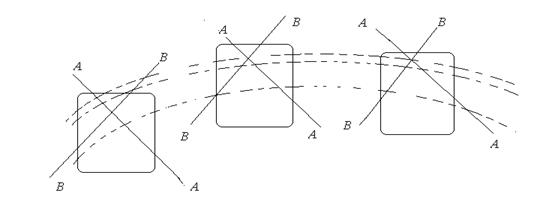
Рис.7.1

Обозначим цифрами 1 и 2 две произвольные точки тела, характеризуемые радиусами-векторам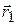и и 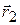. Пусть 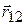– вектор, проведенный из точки 1 в точку 2 (рис.7.2). Расстояние между рассматриваемыми точками неизменно, поэтому 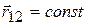. Оно связано с радиусами-векторами точек соотношением 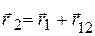. Продифференцировав по времени, получим, что 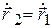, т.е. .

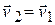Аналогично имеем .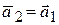

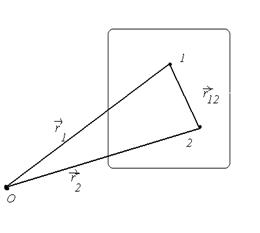Рис.7.2

Таким образом, все точки тела получают за один тот же промежуток времени равные по модулю и направлению перемещения, вследствие чего скорости и ускорения всех точек в каждый момент времени оказываются одинаковыми. Отсюда следует, что при поступательном движении траектории всех точек идентичны и могут быть совмещены параллельным переносом. Поэтому достаточно определить движение одной из точек тела (например, его центра масс) для того, чтобы охарактеризовать полностью движение всего тела.

Следует также отметить, что в случае поступательного движения уравнение (7.6) будет определять ускорение не только центра масс, но и любой другой точки тела.

4. Вращательное движение твердого тела

При вращательном движении все точки тела движутся по подобным траекториям, центры которых лежат на одной и той же прямой, называемой осью вращения (рис.7.3). Окружности, по которым движутся точки тела, лежат в плоскостях, перпендикулярных к этой оси.

O¢

Q

P

O

Рис.7.3.

Положение вращающегося тела может быть определено двугранным углом 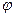, между двумя полуплоскостями, проходящими через ось вращения. Одна плоскость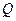 неподвижна относительно системы координат, другая 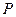связана с телом и вращается вместе с ним. Знак 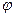определяют по правилу правого винта.

Закон вращения твердого тела определяется уравнением:

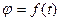(7.7)

Следуя кинематике движения точки по окружности, рассмотренной в предыдущих разделах, вращательное движение твердого тела можно характеризовать угловой скоростью, т.е. скоростью изменения угла поворота:

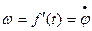(7.8)

Чтобы охарактеризовать не только быстроту вращения, но также и ориентацию оси вращения в пространстве и направление вращения, вводят векторную величину 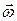, модуль которой определяется формулой (7.8). Направлен вектор 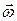вдоль оси вращения, причем так, что направление вращения и направление 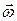образуют правовинтовую систему: если смотреть вслед вектору 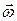, вращение представляется происходящим по часовой стрелке. (Рис.7.4). Определенная таким образом векторная величина 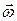называется угловой скоростью тела.

ω

R

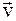
R

Рис.7.4.

Поскольку направление угловой скорости определяется условно, 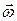является псевдовектором.

Быстрота изменения угловой скорости со временем характеризуется угловым ускорением, т.е.:

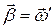(7 .9)

Как и угловая скорость, угловое ускорение является псевдовектором.

Как видно из формулы (7.9), направление 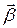определяется направлением изменения угловой скорости 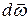. Если угловая скорость растет со временем, т.е. вращение ускоренное, направления 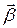и 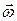совпадают, если же вращение замедленное, направления 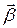и 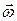противоположные (рис. 7.5).