МАТЕМАТИЧЕСКИЕ ЗАДАЧИ ЭНЕРГЕТИКИ И КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ
И СВЯЗИ
Кафедра электроснабжения промышленных предприятий
МАТЕМАТИЧЕСКИЕ ЗАДАЧИ ЭНЕРГЕТИКИ И КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
Методические указания к выполнению лабораторных работ
для студентов электроэнергетических специальностей
Алматы 2004
АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ
Кафедра электроснабжения промышленных предприятий
УТВЕРЖДАЮ
Проректор по учебно-методической работе
______________________
“___”_________________2004 г.
МАТЕМАТИЧЕСКИЕ ЗАДАЧИ ЭНЕРГЕТИКИ И
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ
Методические указания к выполнению лабораторных работ
для студентов электроэнергетических специальностей
СОГЛАСОВАНО Рассмотрено и одобрено на
Начальник УМО заседании кафедры ЭПП
________________ Протокол № _5__
“___”___________2004г. от “_09_”_января__ 2004г.
Зав. кафедрой ЭПП,
д.т.н., профессор
_____________А.В. Болотов
Редактор Составители:
Старший преподаватель
________________ кафедры ЭПП
__________Н.А. Туканова
“___”___________2004г. Инженер кафедры ЭПП
___________М.М. Махмат
Алматы 2004
СОСТАВИТЕЛИ: Н.А. Туканова, М.М. Махмат. Математические задачи энергетики и компьютерное моделирование. Методические указания к выполнению лабораторных работ для студентов электроэнергетических специальностей - Алматы, АИЭС, 2004. - 34 с.
Методические указания по курсу «Математические задачи энергетики и компьютерное моделирование», включают задания на выполнение лабораторных работ, исходные данные, указания и перечень рекомендуемой литературы.
Методические указания предназначены для студентов очного и заочного обучения.
Ил. 6, табл. 14, библиогр. - 11 назв.
Рецензент: к.т.н., доцент С.А. Бугубаев
Печатается по плану издания Алматинского института энергетики и связи на 2004 год.
|
Алматинский институт энергетики и связи 2004г.
Введение
С развитием промышленности получили дополнительное развитие электрические системы. Чтобы управлять и развивать электрические системы на помощь приходят математические методы прогнозирования, анализа и оптимизации. Решение оптимизационных задач очень важно для инженера-энергетика. Здесь необходимо учесть, что управление энергосистемой и её проектирование должны обеспечивать не только необходимые значения параметров режима, но и максимальную экономичность режима системы в целом при полном удовлетворении потребителей электроэнергией.
Зная алгоритм решения задачи линейного программирования, можно составить программу ее решения на ЭВМ. На сегодняшний день существуют много языков программирования (Pascal, Delhpi, С++, FoxPro, Basic)с помощью которых можно составлять программы для решения задач линейного программирования, математической статистики и т.д. Однако такие программы составить достаточно сложно, поэтому студентам предлагается решить поставленные задачи (на симплекс метод, транспортные задачи, задачи динамического программирования, сетевого моделирования) с помощью специально разработанной программы ПЭР (Пакет экономических расчетов).
При расчете оптимизационных режимов электроэнергетических систем неоценимую помощь оказывают универсальные компьютерные программы-симуляторы электрических систем. Они позволяют на модели произвести экспериментальные исследования, которые сложно и трудоемко выполнять в реальной системе.
Лабораторная работа № 1
Решение систем линейных уравнений и нахождение оптимальных решений с помощью Симплекс метода
1.1 Цель работы
Целью настоящей работы является решение математических задач энергетики с помощью линейного программирования.
1.2 Порядок проведения работы
1.2.1 Найти первоначальный опорный план.
1.2.2 Составить симплекс - таблицу (см. пример таблица 1.6.1).
1.2.3 Определить оптимальность опорного плана и при необходимости перейти к новому опорному плану.
1.2.4 Определить направляющие столбцы и строки.
1.2.5 По методу Жордана - Гаусса определить положительные компоненты нового опорного плана и записать в новой симплекс-таблице.
1.2.6 Проверить план на оптимальность. Если план не оптимален, то вернуться к пункту 1.2.3, а в случае оптимального плана или неразрешимости плана процесс решения заканчивается.
1.3 Оформление результатов работы
Отчет должен содержать:
1.3.1 Исходные данные в виде уравнения функции и системы линейных уравнений.
1.3.2 Первоначальный опорный план, записанный в виде симплекс-таблицы.
1.3.3 Все этапы решения (все симплекс – таблицы) до получения оптимального плана или неразрешимости плана.
1.4 Методические указания
Симплексный метод решения задачи линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функций возрастает (при условии, что данная задача имеет оптимальный план и каждый ее опорный план является невырожденным). Рассмотрим задачу, для которой требуется найти максимальное значение функции
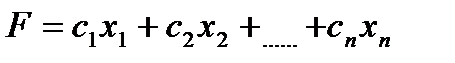

при условиях
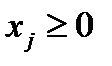
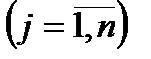 ,
,
где, 
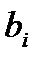
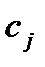
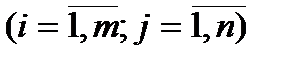 ,(
,( 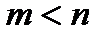 и
и  )- заданные постоянные числа. Векторная форма данной задачи имеет следующий вид
)- заданные постоянные числа. Векторная форма данной задачи имеет следующий вид
 (1.1)
(1.1)
при условиях
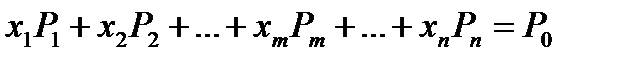 (1.2)
(1.2)
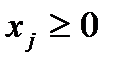 (
( 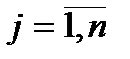 ), (1.3)
), (1.3)
где  ,
, 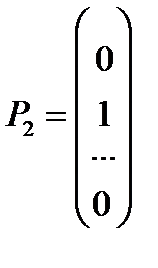 ,
, 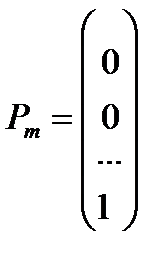 ,
, 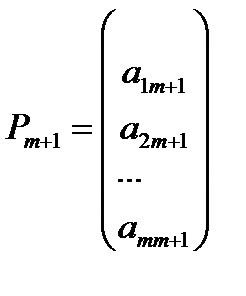 ,
, 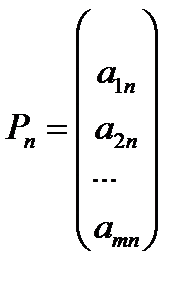 ,
,  .
.
Так как  , то по определению опорного плана
, то по определению опорного плана 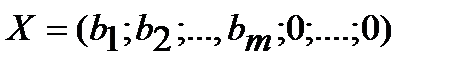 является опорным планом данной задачи (последние
является опорным планом данной задачи (последние 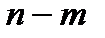 компонентов вектора
компонентов вектора 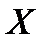 равны нулю). Этот план определяется системой единичных векторов
равны нулю). Этот план определяется системой единичных векторов 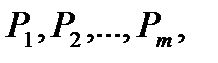 которые образуют базис
которые образуют базис 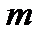 -мерного пространства. Поэтому каждый из векторов
-мерного пространства. Поэтому каждый из векторов 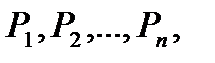 а также вектор
а также вектор 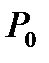 могут быть представлены в виде линейной комбинации векторов данного базиса. Пусть
могут быть представлены в виде линейной комбинации векторов данного базиса. Пусть 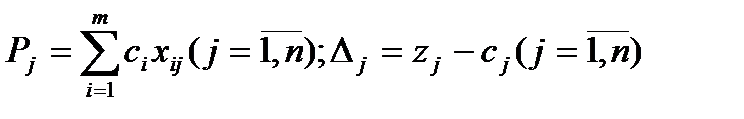 . Так как векторы
. Так как векторы 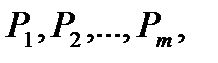 - единичные, то
- единичные, то 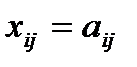 и
и 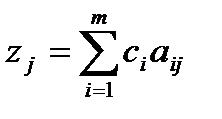 , а
, а 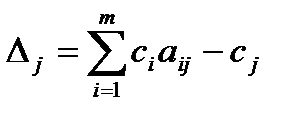 .
.
Признаки оптимальности опорного плана:
1) Опорный план  задачи (1.2)-(1.3) является оптимальным, если
задачи (1.2)-(1.3) является оптимальным, если 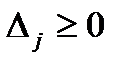 для любого
для любого 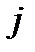 (
(  ).
).
2) Если 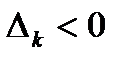 для некоторого и среди чисел
для некоторого и среди чисел 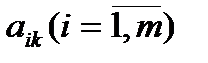 нет положительных
нет положительных 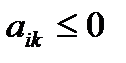 , то целевая функция (1.1) задачи (1.2)-(1.3) не ограничена на множестве ее планов.
, то целевая функция (1.1) задачи (1.2)-(1.3) не ограничена на множестве ее планов.
3) Если опорный план 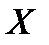 задачи (1.2)-(1.3) не вырожден и
задачи (1.2)-(1.3) не вырожден и 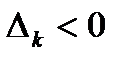 , но среди чисел
, но среди чисел 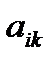 есть положительные (не все
есть положительные (не все 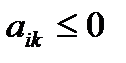 ), то существует опорный план
), то существует опорный план 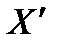 такой, что
такой, что 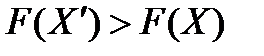 .
.
1.4.1 Этапы нахождение оптимального опорного плана симплекс-методом:
1 Найти опорный план
2 Составить симплекс – таблицу (таблица 1.6.1)
3 Проверить опорный план на оптимальность. Если имеется ли хотя бы одно отрицательное число 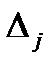 , то либо устанавливают неразрешимость задачи, либо переходят к новому опорному плану. Если нет, то найденный опорный план оптимален.
, то либо устанавливают неразрешимость задачи, либо переходят к новому опорному плану. Если нет, то найденный опорный план оптимален.
4 Найти направляющие столбец и строку. Направляющий столбец определяется наибольшим по абсолютной величине отрицательным числом 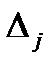 , а направляющая строка - минимальным из отношений компонент столбца вектора
, а направляющая строка - минимальным из отношений компонент столбца вектора 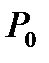 к положительным компонентам направляющего столбца.
к положительным компонентам направляющего столбца.
5 По методу Жордана - Гаусса определить положительные компоненты нового опорного плана, коэффициенты разложения векторов  по векторам нового базиса и числа
по векторам нового базиса и числа 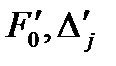 . Все числа записать в новой симплекс-таблице.
. Все числа записать в новой симплекс-таблице.
6 Проверить план на оптимальность. Если план не оптимален, то возвращаемся к 4 этапу, а в случае оптимального плана или неразрешимости плана процесс решения заканчивается.
1.5 Задание и исходные данные
Требуется найти максимальное или минимальное значение функции
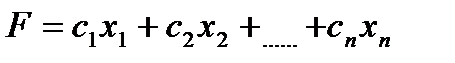
при условиях

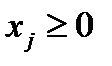
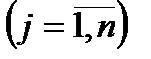 ,
,
где, 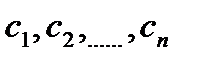 и f(x)
и f(x) 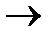 min или max студент выбирает под начальной буквой фамилий, а элементы
min или max студент выбирает под начальной буквой фамилий, а элементы 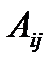 ,
, 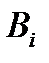 и знаки ограничений выбираем по последней цифре номера зачетной книжки.
и знаки ограничений выбираем по последней цифре номера зачетной книжки.
Таблица 1.5.1 – Исходные данные
| Начальная буква фамилии студента | А, Д | Б, Е | В, Г, Я | Ж, З, И, Л | К | М, О | Н, П | Р, Т, У, Ф | С, Ч | Х, Ш, Щ, Э, Ю |
| Элементы целевой функций | ||||||||||
| C1 | -1 | -4 | ||||||||
| C2 | -2 | -2 | ||||||||
| C3 | -1 | -1 | -1 | -3 | -3 | |||||
| C4 | -1 | -6 | - | - | -1 | - | - | |||
| f(x) | max | min | max | min | max | min | max | min | max | min |
1.6 Используя программный продукт «Пакет экономических расчетов» рассмотрим решение примера 1.
Дано:

Все таблицы получены с помощью пакета экономических расчетов. Для этого открываем папку С/Program Files/ПЭР/Per.exe, открываем файл Per.exe и при нажатие любую клавишу зайдем в главную меню программы. В главном меню предложены 8 видов задач (программ) математического программирования, выбор программы производится клавишами: вниз, вверх и enter.
Таблица 1.5.2 – Исходные данные
| Элементы Ai, Bj ,Cij | ||||||||||||||
| Мощность источников Aij | a11 | -1 | |||||||||||||
| a12 | -1 | -1 | -1 | ||||||||||||
| a13 | -4 | -3 | |||||||||||||
| a14 | -6 | -5 | -1 | - | - | -1 | - | - | |||||||
| a21 | -9 | ||||||||||||||
| a22 | -6 | -3 | -5 | ||||||||||||
| a23 | -3 | -3 | -1 | ||||||||||||
| a24 | -8 | -1 | - | - | - | - | |||||||||
| a31 | -1 | -4 | |||||||||||||
| a32 | -5 | -3 | |||||||||||||
| a33 | -2 | -2 | |||||||||||||
| a34 | -4 | - | - | -2 | - | - | |||||||||
| Мощность потребителей Bj | b1 | -5 | |||||||||||||
| b2 | |||||||||||||||
| b3 | |||||||||||||||
| b4 | - | - | - | - | - | - | - | - | - | - | |||||
| Знаки ограничений ( ≤ ; ≥; =) | = | ≤ | = | ≥ | ≤ | = | ≤ | ≤ | = | ≤ | |||||
| = | ≤ | = | ≤ | = | = | ≤ | ≤ | = | ≥ | ||||||
| = | ≤ | = | ≤ | ≥ | = | ≤ | ≤ | = | ≥ |
Для нашего примера мы выбираем программу (задачу) «Линейное программирование», далее заходим в окно /Функции/Ввод новой задачи/, где даем любое имя своей задачи (файл/<Лаб1>) и нажатием enter, выводится окно /Ввод данных Лаб1/. В этом окне предложено 7 пунктов соглашения, в дальнейшим вводим условие максимизации (минимизации) задачи - вводим <1>, количество переменных - <4>, ограничений - < 2>. Нажимая пробел, мы открываем окно, куда вводятся элементы целевой функции и ограничения (нажимаем enter, пробел и любую клавишу), выбираем в окне /Функций/ -<решение задачи> и /открываются опции меню для решение задачи Лаб1/, там выбираем опцию /решить и вывести все таблицы/, далее поэтапно получаем таблицу 1.6.1 "Начальную таблицу" и все итерации.
Таблица 1.6.1 - Начальная таблица
| Базис | C(j) | X1 | X2 | X3 | X4 | A1 | A2 | B(i) | B(i) |
| 8.000 | 6.000 | - M | - M | A(i,j) | |||||
| A1 | - M | 5.000 | 2.000 | 1.00 | 1.00 | 0.00 | 20.00 | ||
| A2 | - M | 6.000 | 12.000 | 1.00 | 1.00 | 72.00 | |||
| C(j)-Z(j) | 8.000 | 6.000 | |||||||
| * Big M | -1.00 | -1.00 | -92.0 |
где Х1,…Х4-переменные элементы системы; C(j)- базисные коэффициенты целевой функций; Х1,…,Х4 - коэффициенты ограничений; C(j)-Z(j)- коэффициенты целевой функции.
Таблица 1.6.2 – Итерация 1
| Базис | C(j) | X1 | X2 | X3 | X4 | A1 | A2 | B(i) | B(i) |
| 8.000 | 6.000 | - M | - M | A(i,j) | |||||
| A1 | - M | 5.000 | 2.000 | 1.00 | 1.00 | 0.00 | 20.00 | 10.00 | |
| A2 | - M | 6.000 | 12.000 | 1.00 | 1.00 | 72.00 | 6.000 | ||
| C(j)-Z(j) | 8.000 | 6.000 | |||||||
| * Big M | 11.00 | 14.00 | 1.00 | 1.00 | -92.0 |
ТЕКУЩЕЕ ЗНАЧЕНИЕ ЦЕЛЕВОЙ ФУНКЦИИ (Max.) = 0 + (-92BigM)
ВВОДИМ : X2 Выводим: A2
Таблица 1.6.3 - Итерация 2
| Базис | C(j) | X1 | X2 | X3 | X4 | A1 | A2 | B(i) | B(i) |
| 8.000 | 6.000 | - M | - M | A(i,j) | |||||
| A1 | - M | 4.000 | 1.00 | -.167 | 1.00 | -.167 | 8.000 | 2.000 | |
| X2 | 6.000 | 0.500 | 1.000 | 0.083 | 0.083 | 6.000 | 12.00 | ||
| C(j)-Z(j) | 5.000 | -.500 | -.500 | 36.00 | |||||
| * Big M | 4.000 | 1.00 | -.167 | -1.17 | -8.00 |
ТЕКУЩЕЕ ЗНАЧЕНИЕ ЦЕЛЕВОЙ ФУНКЦИИ (Max.) = 36 + (-8BigM)
ВВОДИМ : X1 Выводим: A1
Таблица 1.6.4 – Конечная таблица
| Базис | C(j) | X1 | X2 | X3 | X4 | A1 | A2 | B(i) | B(i) |
| 8.000 | 6.000 | - M | - M | A(i,j) | |||||
| X1 | 8.000 | 1.000 | 0.250 | -.042 | 0.250 | -.042 | 2.000 | ||
| X2 | 6.000 | 1.000 | -.125 | 0.104 | -.125 | 0.104 | 5.000 | ||
| C(j)-Z(j) | -1.25 | -.292 | -1.25 | -.292 | 46.00 | ||||
| * Big M | -1.00 | -1.00 |
(Max.) Оптимальная величина ЦФ = 46
Таблица 1.6.5 – Итоговый результат для контрольного примера
| Переменн No.Имена | РЕШЕНИЕ | Двойственн.оцен | Переменн No.Имена | РЕШЕНИЕ | Двойственн.оцен |
| 1 X1 2 X2 3 X3 | 2.0000 5.0000 0.0000 | 0.0000 0.0000 1.2500 | 4 4 X4 5 5 A1 6 A2 | 0.0000 0.0000 0.0000 | 0.2917 0.2917 0.2917 |
| MAX величина цел.ф-и = 46 Итерац.= 2 |
1.7 Контрольные вопросы
1.7.1 Как строится первоначальный опорный план задачи линейного программирования и проверяется на оптимальность?
1.7.2 Как определить вектор, подлежащий исключению из базиса?
1.7.3 Какой метод решения систем линейных уравнений лежит в основе симплекс - метода?
1.7.4 Какой элемент называется разрешающим?
1.7.5 Как определяется вектор для включения в базис, если первоначальный план не является оптимальным?
1.7.6 Этапы нахождение оптимального опорного плана симплекс – методом?
Лабораторная работа № 2
Определение оптимального плана электроснабжения потребителей с помощью транспортных задач
2.1 Цель работы
Целью настоящей работы является составление такого плана перевозок, который обеспечивал бы минимальные стоимости передачи (перевозок) единицы мощности энергии, и который удовлетворял бы спрос всех потребителей за счет распределения энергии, произведенной всеми пунктами источников питания.
2.2 Порядок проведения работы
2.2.1 Проверить транспортную задачу на условие разрешимости и составить матрицу планирования (см. пример таблица 2.6.1).
2.2.2 Найти первоначальный опорный план методом северо-западного угла с помощью пакета экономических расчетов.
2.2.3 Определить оптимальность опорного плана и при необходимости перейти к новому опорному плану.
2.2.4 Построить системы потенциалов и проверить выполнение условия оптимальности для незанятых клеток.
2.2.5 Выбрать клетку, в которую необходимо послать перевозку и построить замкнутый цикл, определив величины перераспределения груза.
2.2.7 Новый план проверить на оптимальность. Если план неоптимальный, то перейти к п. 2.2.5, в противном случае процесс решения заканчивается.
2.3 Оформление результатов работы
Отчет должен содержать:
2.3.1 Исходные данные оформляются как в примере 2.
2.3.2 Все таблицы должны быть заполнены, итоговый результат записан.
2.4 Методические указания
В 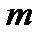 - пунктах источниках питания
- пунктах источниках питания  находится однородный продукт, (энергия) в количествах, соответственно мощностью источников
находится однородный продукт, (энергия) в количествах, соответственно мощностью источников 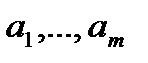 , который должен быть доставлен
, который должен быть доставлен  - потребителям
- потребителям 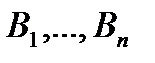 в количествах, соответственно мощности потребителей
в количествах, соответственно мощности потребителей  . Известны стоимость передачи единицы продукта
. Известны стоимость передачи единицы продукта  , связанные с перевозкой единицы продукций из
, связанные с перевозкой единицы продукций из 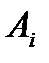 пункта в пункт
пункта в пункт 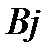 .
.
Требуется составить такой план перевозок, который обеспечивал бы при минимальных стоимости передачи (перевозок) единицы мощности энергии и удовлетворял бы спрос всех потребителей за счет распределения энергии, произведенной всеми пунктами источников питания.
Необходимым и достаточным условием разрешимости задачи является равенство (2.1*)
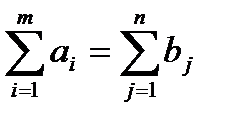 (2.1*)
(2.1*)
Если 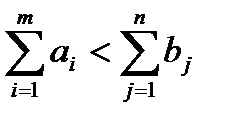 или
или 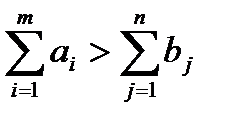 , то имеем транспортную задачу с открытой моделью.
, то имеем транспортную задачу с открытой моделью.
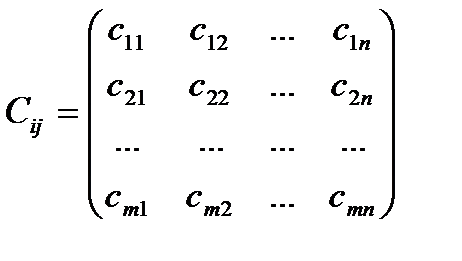
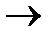 - матрица расходов (затрат) или матрица стоимости передачи единицы мощности.
- матрица расходов (затрат) или матрица стоимости передачи единицы мощности.
Планом ТЗ называется 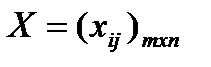 , где каждое число
, где каждое число 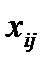 обозначает количество единиц груза, который надо доставить из
обозначает количество единиц груза, который надо доставить из 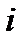 -го пункта отправления в
-го пункта отправления в 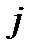 -го назначения.
-го назначения.
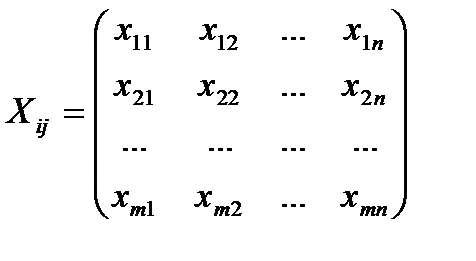
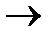 - матрица перевозок (передач).
- матрица перевозок (передач).
Общие суммарные затраты, связанные с реализацией плана перевозок можно представить целевой функцией:
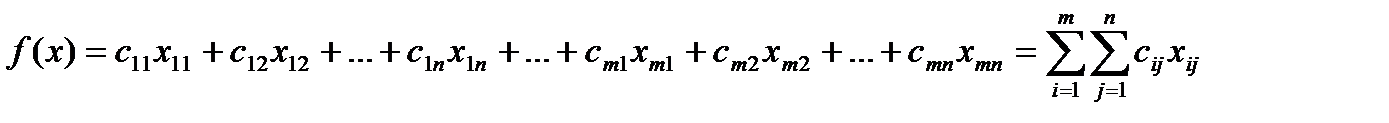 (2.1)
(2.1)
Математическая модель:
 (
( 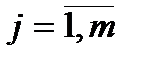 )
)
(2.2)
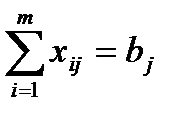 (
( 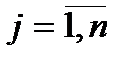 )
)
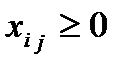 (
( 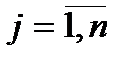 ;
; 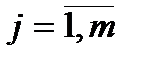 ) (2.3)
) (2.3)
Система ограничений задачи содержит  уравнений с m n переменными
уравнений с m n переменными  .
.
Необходимым и достаточным условием решения задачи является то, что ранг матрицы ТЗ должен быть на единицу меньше числа уравнений, т.е.  .
.
Из условия следует, что каждый опорный план имеет 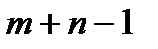 базисных переменных и
базисных переменных и 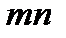 -(
-( 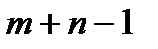 )=
)= 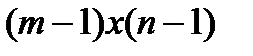 свободных переменных, равных нулю.
свободных переменных, равных нулю.
2.4.1 Исходный опорный план можно получить следующими методами
2.4.1.1 Метод северо-западного угла. Для составления исходного опорного плана, заполняем таблицу с левого верхнего (северо-западного) угла, двигаясь далее по строке вправо или по столбцу вниз.Этот метод обычно оказывается далеким от оптимальности, так как не учитывает величины 
затрат (расходов)  .
.
2.4.1.2 Методом минимального элемента.Сущностьего состоит в том, что заполнение начинается с клетки, которая соответствует минимальному элементу матрицы стоимости передачи единицы мощности (расходов).
Полученные опорные решения транспортной задачи необходимо проверить на оптимальность с помощью метода потенциалов.
2.4.2 Проверка опорного решения на оптимальность проводится с помощью метода потенциалов.
Первоначальный опорный план оптимален при следующих условиях:
1) для каждой занятой клетки сумма потенциалов должна быть равна стоимости единицы перевозок, стоящей в этой клетке
U*i + V*j =Cij (2.4)
2) для каждой незанятой клетки сумма потенциалов должна быть меньше или равна единицы перевозки, стоящей в этой клетке
U*i + V*j ≤Cij (2.5)
Если хотя бы одна незанятая клетка не удовлетворяет условию, то опорный план является неоптимальным и его можно улучшить, вводя в базис вектор, соответствующий клетке, для который нарушается условие оптимальности (в клетку max [(U*i+V*j)-Cij] надо переместить некоторое количество единиц груза, т.е. загрузить).
2.5 Задание и исходные данные
Пусть имеются A 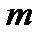 - электростанций с мощностями
- электростанций с мощностями 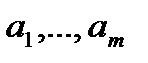 , и B
, и B  -потребители с мощностью потребление
-потребители с мощностью потребление  . Дана матрица стоимости передачи единицы мощности
. Дана матрица стоимости передачи единицы мощности 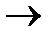
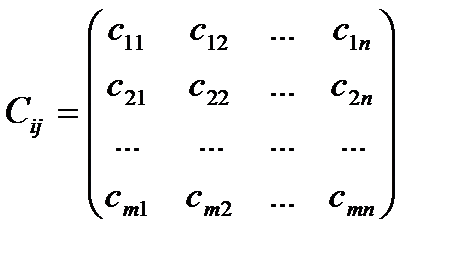 . Требуется найти минимальную стоимость передачи электроэнергии от электростанций к потребителям.
. Требуется найти минимальную стоимость передачи электроэнергии от электростанций к потребителям.
Для этого: 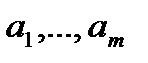 мощность электростанций,
мощность электростанций,  - мощность потребителей,
- мощность потребителей, 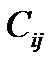 -элементы выбирают по предпоследней цифре номера зачетной книжки по таблице 2.5.1.
-элементы выбирают по предпоследней цифре номера зачетной книжки по таблице 2.5.1.
2.6 Пример выполнения задания
Используя программный продукт ПЭР (Пакет экономических расчетов), рассмотрим пример 2.
Дано:
S1 =30 D1=20, D4=10
S2=40 D2=25
S3=20 D3=35
Cij = 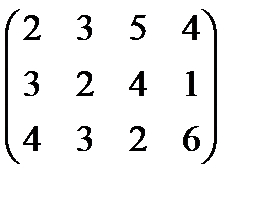
Таблица 2.5.1 – Исходные данные
|
| ЭлементыAi, Bj , Cij | |||||||||||
| Мощность источников Ai | a1 | ||||||||||
| a2 | |||||||||||
| a3 | |||||||||||
| a4 | - | - | - | - | - | ||||||
| a5 | - | - | - | - | - | - | - | - | - | - | |
| Мощность потребителей Bj | b1 | ||||||||||
| b2 | |||||||||||
| b3 | |||||||||||
| b4 | |||||||||||
| b5 | - | - | - | - | - | ||||||
| Стоимость передачи единицы мощности C ij | c11 | ||||||||||
| c12 | |||||||||||
| c13 | |||||||||||
| c14 | |||||||||||
| c15 | - | - | - | - | - | ||||||
| c21 | |||||||||||
| c22 | |||||||||||
| c23 | |||||||||||
| c24 | |||||||||||
| c25 | - | - | - | - | - | ||||||
| c31 | |||||||||||
| c32 | |||||||||||
| c33 | |||||||||||
| c34 | |||||||||||
| c35 | - | - | - | - | - | ||||||
| c41 | - | - | - | - | - | ||||||
| c42 | - | - | - | - | - | ||||||
| c43 | - | - | - | - | - | ||||||
| c44 | - | - | - | - | - | ||||||
| c45 | - | - | - | - | - | - | - |
Для нашего примера мы выбираем программу (задачу) «Транспортная задача», далее заходим в окно /Функций/ Ввод новой задачи/, где даем любое имя своей задачи. Задача называется - (файл/<Лаб2>) и нажатием enter, выводится окно /Ввод данных Лаб1/. В этом окне предложено 7 пунктов соглашения, в дальнейшим вводим условие максимизации =1 (минимизации=2) задачи вводим <1>, количество поставщиков - <3>, потребителей - <4>. Нажимая пробел, мы открываем окно, куда вводится объем поставок и запрос потребителей (нажимаем enter, пробел и любую клавишу), заходим в окно, куда вводятся коэффициенты матрицы перевозок единицы мощности (нажимаем enter, пробел и любую клавишу), выбираем в окне /Функций/-<решение задачи> и /открываются опции меню для решение задачи Лаб2/, там выбираем опцию /решить и вывести каждую итерацию/, далее поэтапно получаем "Начальную таблицу", т.е. матрицу планирования и все итерации. На последнем итерации "Конечная таблица", нажимая любую клавишу, выводим конечное решение, т.е. выводим итоговый результат для Лаб2 .
Таблица 2.6.1 – Начальная таблица «Матрица планирования»
| Из\В | D1 | D2 | D3 | D4 | Пост | Ui |
| S1 | 2 | 3 | 5 | 4 | ||
| S2 | 3 | 2 | 4 | 1 | ||
| S3 | 4 | 3 | 2 | 6 | ||
| Потр | ||||||
| Vj |
Таблица 2.6.2 - Итерация 1
| Из\В | D1 | D2 | D3 | D4 | Пост | Ui |
| S1 | 20 2 | 10 3 | 5 | 4 | ||
| S2 | 3 | 15 2 | 25 4 | ** 1 | -1 | |
| S3 | 4 | 3 | 10 2 | 10 6 | -3 | |
| Потр | ||||||
| Vj | 9 |
Текущая MIN величина ЦФ = 280 с e( 2, 4) =-7
Таблица 2.6.3 – Конечная таблица
| Из\В | D1 | D2 | D3 | D4 | Пост | Ui |
| S1 | 20 2 | 10 3 | 5 | 4 | ||
| S2 | 3 | 15 2 | 15 4 | 10 1 | -1 | |
| S3 | 4 | 3 | 20 2 | 6 | -3 | |
| Потр | ||||||
| Vj |
MIN величина ЦФ = 210
Таблица 2.6.4 – Итоговый результат для ЛАБ 2
| ИЗ | В | Поставка | Оценка | ИЗ | В | Поставка | Оценка |
| S1 | D1 | 20.0 | 2.000 | S2 | D3 | 15.0 | 4.000 |
| S1 | D2 | 10.0 | 3.000 | S2 | D4 | 10.0 | 1.000 |
| S1 | D3 | 0.0 | 5.000 | S3 | D1 | 0.0 | 4.000 |
| S1 | D4 | 0.0 | 4.000 | S3 | D2 | 0.0 | 3.000 |
| S2 | D1 | 0.0 | 3.000 | S3 | D3 | 20.0 | 2.000 |
| S2 | D2 | 15.0 | 2.000 | S3 | D4 | 0.0 | 6.000 |
MIN величина ЦФ = 210 (возм. неоднозн.) Итераций = 1
2.7 Контрольные вопросы
2.7.1 Построение первоначального опорного плана транспортной задачи линейного программирования (методы построения).
2.7.2 Сформулируйте транспортную задачу линейного программирования и запишите ее математическую модель.
2.7.3 Дайте определение открытой и закрытой транспортных задач, в чем отличительные особенности их решения?
2.7.4 Метод потенциалов.
2.7.5 Условия оптимальности плана транспортной задачи линейного программирования?
Лабораторная работа № 3
Имитационные исследования трансформаторов в среде Electronics Workbench.
3.1 Цель работы
3.1.1 Изучить принцип действия и основные закономерности электромагнитных процессов, происходящие в трансформаторах.
3.1.2 В среде Electronics Workbench имитировать процесс исследования трансформаторов в режимах холостого хода, короткого замыкания и под нагрузкой.
3.1.3 Провести анализ осциллограмм тока I2(t), напряжения U2(t) при активной, индуктивной и смешанной нагрузке трансформатора.
3.2 Средства для имитационного исследования трансформаторов
В лабораторной работе используются следующие элементы Electronics Workbench:
¨ ¨ источники переменного напряжения;
¨ ¨ резисторы;
¨ ¨ конденсаторы;
¨ ¨ катушки индуктивностей;
¨ ¨ трансформаторы;
¨ ¨ вольтметры;
¨ ¨ амперметры;
¨ ¨ осциллографы;
¨ ¨ блок ваттметра.
3.3 Краткие теоретические сведения
Трансформатор состоит из замкнутого стального магнитопровода, на котором располагаются две или несколько обмоток, электрически не соединенные между собой.
Часть магнитопровода, на котором располагаются обмотки, называется стержнем. Обмотка, к которой электрическая энергия подается, называется первичной; другая обмотка, к которой присоединяются приемники энергии, называется вторичной.
3.3.1 Режим холостого хода трансформатора
Подведем к первичной обмотке трансформатора синусоидальное напряжение u1 = U1M sin ωt (рисунок 3.1).
Рассмотрим процессы при разомкнутом рубильнике p2, т.е. когда вторичная обмотка трансформатора не замкнута (режим холостого хода).
Под действием приложенного напряжения в первичной обмотке возникнет переменный ток, который аналогично току в цепи с индуктивностью будет отставать от напряжения по фазе на угол, близкий к 90°, а в магнитопроводе трансформатора возникнет переменный магнитный поток, практически совпадающий по фазе с током и пронизывающий витки обеих обмоток трансформатора. Переменный магнитный поток наводит в первичной и во вторичной обмотках трансформатора э.д.с.
На основании второго правила Кирхгофа, пренебрегая падением напряжения в первичной обмотке, можно определить действующее значение напряжения на зажимах первичной обмотки и действующее значение э.д.с, наведенной в первичной обмотке
U1 = E1 = 4,44 f ω1 ФМ. (3.1)
Мгновенное значение напряжения на зажимах разомкнутой вторичной обмотки равно мгновенному значению е2 . Таким образом,
u2 = e2
U2 = E2 = 4,44 f ω2 ФМ. (3.2)
Схема соединения трансформатора
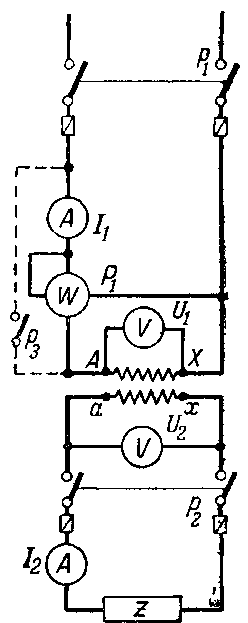
Рисунок 3.1
Отношение э.д.с обмотки высшего напряжения к э.д.с. обмотки низшего напряжения называется коэффициентом трансформации (обозначение k.). При холостом ходе оно равно
k = U1/U2 (3.3)
или

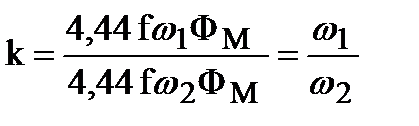 . (3.4)
. (3.4)
Если 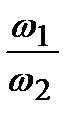 >l трансформатор носит название понижающего,то при
>l трансформатор носит название понижающего,то при 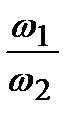 <1 - повышающего. Как было уже упомянуто, ток в первичной обмотке при режиме холостого хода отстает от напряжения на угол φ1, близкий к 90°. Косинус угла φ1 при холостом ходе составляет около 0,1. Величина тока IX при холостом ходе составляет (3 ÷ 8)% номинального тока первичной обмотки. Произведение IX ω1 при холостом ходе называется намагничивающей силой трансформатора и обозначается FX. Таким образом,
<1 - повышающего. Как было уже упомянуто, ток в первичной обмотке при режиме холостого хода отстает от напряжения на угол φ1, близкий к 90°. Косинус угла φ1 при холостом ходе составляет около 0,1. Величина тока IX при холостом ходе составляет (3 ÷ 8)% номинального тока первичной обмотки. Произведение IX ω1 при холостом ходе называется намагничивающей силой трансформатора и обозначается FX. Таким образом,
FX = IX ω1. (3.5)
3.3.2 Работа нагруженного трансформатора
Присоединим ко вторичной обмотке трансформатора приемник энергии. В цепи вторичной обмотки возникнет ток I2. Величина этого тока зависит от E2 и полного сопротивления вторичной цепи. При смешанной индуктивной нагрузке ток I2 отстает по фазе от E2 на угол ψ2.
Токи I1 и I2 сдвинуты по фазе на угол, близкий к 180°.
При неизменном значении первичного напряжения и изменении нагрузки трансформатора Р2 от нуля до номинальной будет увеличиваться как вторичный, так и первичный токи трансформатора, будут увеличиваться и падения напряжения в его обмотках (I1z1 и I2z2), а напряжение на зажимах вторичной обмотки будет уменьшаться.
Если обозначить U2 напряжение на зажимах вторичной обмотки трансформатора при нагрузке, а U2X - при холостом ходе, то величина
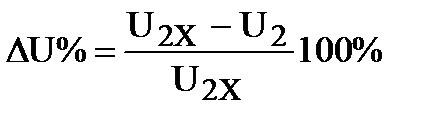 , (3.6)
, (3.6)
называется процентным изменением напряжения трансформатора.
Величина ΔU% зависит не только от величины тока нагрузки, но и от характера нагрузки, т.е. от cos φ2.
Процентное изменение напряжения в современных трансформаторах незначительно, порядка 2¸3%.
3.3.3 Мощность трансформатора и к.п.д.
Первичная мощность трансформатора
Ρ1 = U1 I1 cos φ1. (3.7)
Вторичная мощность трансформатора
Ρ2 = U2 I2 cos φ2. (3.8)
Разность между первичной и вторичной мощностями (P1—P2) представляет собой мощность потерь. Потери в трансформаторе состоят из двух частей: 1) потери в меди обмоток РM и 2) потери в стали трансформатора от гистерезиса и вихревых токов Рст = Рг + Рс.
Потери в стали могут быть определены из опыта холостого хода, т.е., когда рубильник р2 разомкнут, а рубильник p1 замкнут и к трансформатору подведено U1 = U1H. В этом случае ваттметр покажет
РX = Pст + РMX.
Так как потери в меди при холостом ходе РMX ничтожно малы, то
РX = РM. (3.9)
Потери в меди определяются опытом короткого замыкания, когда зажимы вторичной обмотки ах замкнуты накоротко, а к первичной обмотке подведено такое пониженное напряжение UK,при котором токи в обмотках будут номинальными. Это напряжение называется напряжением короткого замыкания и составляет 5 ÷ 12% UH..
Ваттметр измерит мощность РK = РM+Рст.K. Однако, так как UK ≈ 0,05UH,, то индукция в стали ничтожно мала и потерями в стали при коротком замыкании Рст.K можно пренебречь. Тогда
РK = PM . (3.10)
Коэффициент полезного действия трансформатора представляет собой отношение вторичной мощности Р2 к первичной мощности P1, т.е.
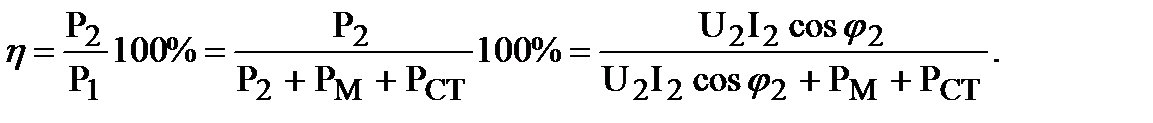 (3.11)
(3.11)
3.4 Содержание лабораторной работы
3.4.1 Схема эксперимента предоставлена на рисунке 3.2 в среде Electronics Workbench.
Режим нагрузки выбирается по варианту, выданному преподавателем, в соответствии с таблицей 3.1.
3.4.2 Включить трансформатор вхолостую и измерить первичное и вторичное напряжения U1, и U2. Измерить мощность холостого хода ΡX и ток холостого хода IX . Подсчитать коэффициент трансформации, потери в стали и отношение (IX/IH)100%.
3.4.3 Произвести опыт короткого замыкания и измерить: напряжение при коротком замыкании UK, мощность короткого замыкания РK, и ток в первичной обмотке I1= IH..
3.4.4 Рассчитать uK = (UK/UH)100%, к.п.д. трансформатора при номинальном токе I1 = IH и a) cos φ2 = 1 и б) cos φ2 = 0,8.
3.4.5 Подключить нагрузку и измерить ток в первичной и вторичной обмотке, напряжение во вторичной обмотке. Как изменились их значения? Зарисовать осциллограмму тока и напряжения во вторичной обмотке.
3.5 Описание работы
Включение трансформатора производится по схеме и ее аналогу на рисунке 3.2. Для опыта холостого хода трансформатора при выключенном рубильнике p2 замыкают рубильник p1 и измеряют IX, PX и U2. Перед включением рубильника токовую цепь амперметра и ваттметра шунтируют проводом малого сопротивления, как показано пунктиром на рисунке 3.1. После включения размыкают рубильник р3 и производят измерения. При опыте необходимо, чтобы подведенное напряжение UХ было равно указанному на щитке трансформатора, т.е. UН. Когда измеряют мощность PX, вольтметр во вторичной цепи должен быть отключен. По полученным данным определяют:
1) коэффициент трансформации k = U1/U2;
2) потери в стали Рст = РX;
3) (IX/I1H)100%; обычно равное (10÷2,5)%IK.
Для опыта короткого замыканиязажимы вторичной обмотки ax должны быть замкнуты накоротко проводом малого сопротивления, а к первичной подводится пониженное напряжение с таким расчетом, чтобы ток в первичной обмотке был равен номинальному (I1 =I1H). После этого измеряют UK, I1H и PK. Тогда подсчитывают:
1) напряжение короткого замыкания uK = (UK/UH)100%, равное обычно (3¸12%)UH
2) потери в меди при номинальном токе ΡМ = РK;
3)К.П.Д. 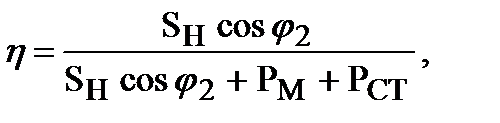
для cos φ2 = 1 и cos φ2 = 0,8.
Здесь
SH = U2HI2H.
Технические данные указаны на щитке трансформатора.
В таблице 3.1 параметры трансформатора и нагрузки обозначены следующим образом:
K – коэффициент трансформации;
LP – индуктивность рассеивания (Гн);
L1 – индуктивность первичной обмотки (Гн);
R1 – сопротивление первичной обмотки (Ом
| <== предыдущая лекция | | | следующая лекция ==> |
| Машиностроительные технологии | | | КОНЦЕПЦИИ СОВРЕМЕННОГО ЕСТЕСТВОЗНАНИЯ |
Дата добавления: 2015-08-11; просмотров: 1348;
