Парабола.
Определение: Параболой называют множество точек плоскости, расстояние от каждой из которых до заданной точки (фокуса) равно расстоянию до заданной прямой (директрисы).
Расположим параболу так, чтобы начало координат находилось посредине между F и директрисой, причем фокус лежал на оси ОХ.
Обозначим расстояние между F и директрисой - p.
Фокус: F(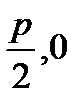 
).
уравнение директрисы: х=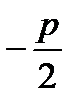 
.
т. М (х, у) - текущая точка параболы.
|
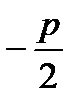
| y |
N(  )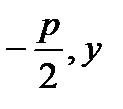
|
|
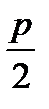
| F |
| M(x, y) |
| х |
По определению параболы: │FM│=│NM│.
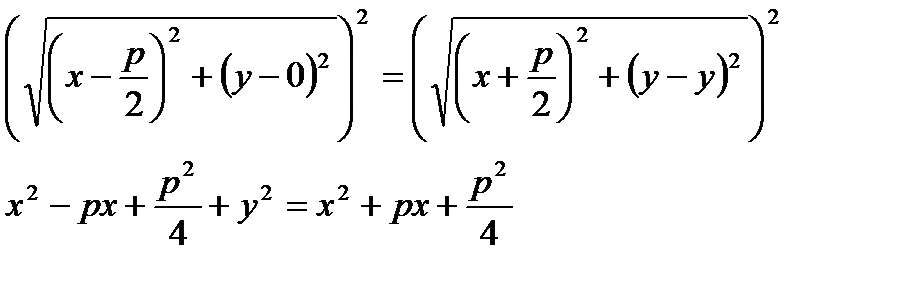
- каноническое уравнение параболы.
Анализ:
Так как уравнение четно по у, то парабола симметрична относительно оси ОХ.
При х= 0: у= 0. С возрастанием х, увеличивается у.
P - параметр параболы.
т. О(0,0) - вершина.
: ось симметрии - ось ОХ, p > 0 -график ; p < 0- график .
Аналогично можно вывести каноническое уравнение параболы с осью симметрии ОУ.
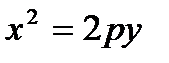: ось симметрии – ось ОУ, p > 0 –график ; p < 0- график .
Дата добавления: 2015-08-11; просмотров: 679;