Эллипс.
Определение: Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух заданных точек (фокусов), есть величина постоянная, равная 2а, большая, чем расстояние между фокусами.
Расположим эллипс так, чтобы фокусы находились на оси ОХ на одинаковом расстоянии от начала координат. Обозначим расстояние между фокусами │F1F2│=2c.
| y |
| c |
| -c |
| F2 |
| F1 |
| M(x, y) |
| x |
F1 (-c, 0) - левый фокус, F2 (с, 0) - правый фокус.
т. М (х, у)- текущая точка эллипса.
По определению: │F1 M│+│F2M│=2a.
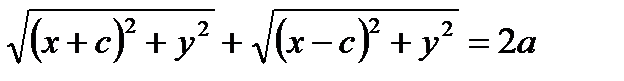
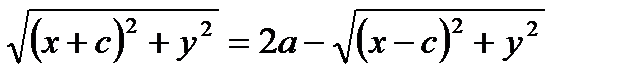
Возведем обе части в квадрат:
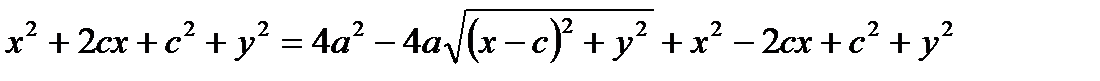
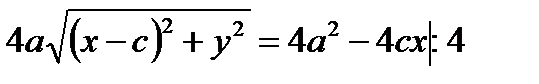
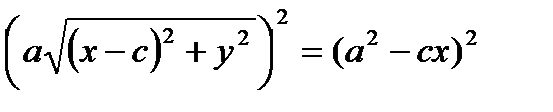
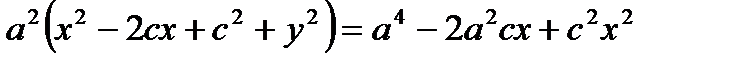
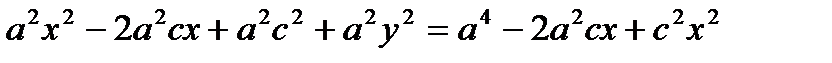
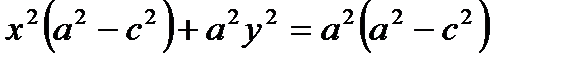
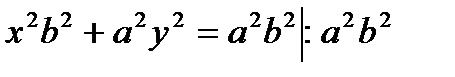
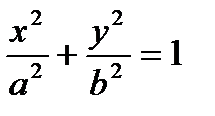 - каноническое уравнение эллипса.
- каноническое уравнение эллипса.
Для построения проанализируем это уравнение:
1) Т.к. уравнение четно по х и у, то эллипс симметричен относительно осей ОХ и ОУ, поэтому достаточно будет построить эллипс в первой четверти и сделать симметрию относительно осей координат.
Выразим из канонического уравнения у через х:
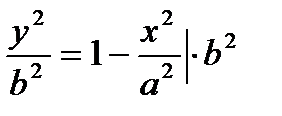
| - |
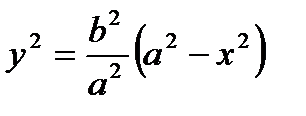
| а |
| -а |
| - |
| + |
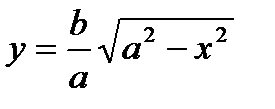
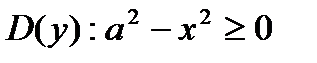
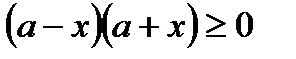
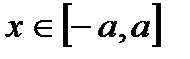
2) Найдем у(0)= b, y(a)= 0. С ростом х, уменьшается у.
Отрезок [0, а] на ОХ - большая полуось, [0, b] - малая полуось эллипса.
т. (а, 0) - правая вершина, т. (-а, 0) - левая вершина, т. (0, b) - верхняя вершина, т. (0, -b) - нижняя вершина, с - фокусное расстояние.
Так как a2-c2= b2, то c2= a2-b2- соотношение, связывающее три параметра эллипса.
Определение: Мерой сжатия эллипса является эксцентриситет: 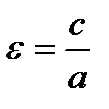 .
.
Для эллипса: 0< 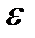 <1.
<1.
Если эксцентриситет стремится к 0, то эллипс будет стремиться к окружности. Если эксцентриситет стремится к 1, то эллипс будет стремиться к отрезку.
Дата добавления: 2015-08-11; просмотров: 653;
