Окружность.
Определение: Окружностью называют множество точек плоскости, удаленных от заданной точки (центра окружности) на заданное расстояние (радиус окружности).
Пусть центр окружности С (а, b) и радиус равен R, т. М (х, у)- текущая точка.
| b |
| а |
| у |
| х |
По определению │СМ│=R.
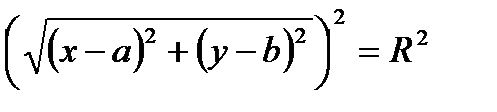 ,
,
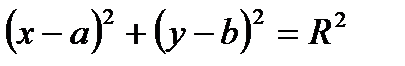 - нормальное уравнение окружности.
- нормальное уравнение окружности.
Если центр окружности находится в начале координат, т.е. С(0;0). Отсюда следует, что 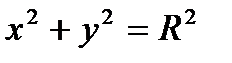 - каноническое уравнение окружности.
- каноническое уравнение окружности.
Замечание:
1) Если в общем уравнении кривой второго порядка отсутствуют произведения x, y и коэффициенты при x2 и y2 равны, то это обязательно уравнение окружности, которое можно получить, выделяя полные квадраты по каждой переменной.
2) Может оказаться, что после выделения полных квадратов уравнение окружности примет вид 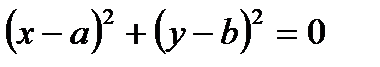 , центр окружности С(а,b), а радиус R= 0. Это уравнение вырожденной окружности. Может оказаться, что
, центр окружности С(а,b), а радиус R= 0. Это уравнение вырожденной окружности. Может оказаться, что 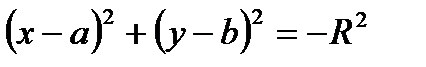 - мнимая окружность (без рисунка).
- мнимая окружность (без рисунка).
3) Через любые три точки, не лежащие на одной прямой можно провести единственную окружность.
Дата добавления: 2015-08-11; просмотров: 744;
