Вопрос 3 – Определение напряжений в грунтовом массиве от действия местной нагрузки на его поверхности.
Распределение напряжений в основании определяется методами теории упругости. Основание при этом рассматривают как упругое полупространство, бесконечно простирающееся во все стороны от горизонтальной поверхности загружения. Напряжение стабилизировано.
В основе решения задачи о распределении напряжений в упругом полупространстве под действием местной нагрузки лежит действие вертикальной сосредоточенной силы, приложенной к поверхности упругого полупространства (1885 г., Ж. Буссинеск).
Это решение позволяет определить все компоненты напряжений и деформаций в любой точке полупространства Мот действия силы Р.
Допустим, что положение точки М определяется полярными координатами (Рисунок 9, а) R и β системы координат с началом в точке приложения силы Р. Под действием силы Р точка М переместится в направлении радиуса R на величину S1. Чем дальше от точки О будет расположена точка М, тем меньше будет ее перемещение. При R = ∞перемещение точки М будет равно 0.
Для практических расчетов (в частности, для определения осадки фундамента) наибольшее значение имеют вертикальные напряжения:
σ z = (K / z2 ) . P , (3.4)



Рисунок 9 – Расчетные схемы основных задач:
а) задача Буссинеска;
б) задача о действии нескольких сил;
в) задача Фламана
где К - коэффициент влияния. Его величина зависит только от отношения r / z , для разных соотношений составлены специальные таблицы. Коэффициент К можно определить по формуле:
К = (3 / 2π ) / (1 / [1 + (r / z)2 ] 5/2 , (3.5)
Действие нескольких сосредоточенных сил (Рисунок 9, б). Используя принцип суперпозиции, определяют значение вертикального сжимающего напряжения в точке М при действии нескольких сосредоточенных сил, приложенных на поверхности:
n
σ z = (K1 / z2 ) . P1 + (K2 / z2 ) . P2 + … + (Kn / z2 ) . Pn = (1 / z2 ) . ∑ Ki . Pi , (3.6)
i = 1
где Ki определяется по формуле (3.5) в зависимости от соотношенияri / z, причем координата z постоянна для данной точки М.
Решение задачи по Фламану для вертикальной сосредоточенной силы Р в условиях плоской задачи имеет вид (3.7):
σ z = (2Р / π ) . ( z3 / r4 ); σ х = (2Р / π ) . ( х 2 z / r4 ); τ хz = (2Р / π ) . ( х z2 / r4 ), (3.7)
где r 2 = х 2 + z 2 .
Зная закон распределения нагрузки на поверхности в пределах контура загружения, можно, интегрируя выражение (3.6) в пределах этого контура, определить значения напряжений в любой точке основания для случаев осесимметричной и пространственной нагрузки, а интегрируя выражение (3.7) - для случая плоской нагрузки.
Вопрос 4 – Влияние формы и площади фундамента в плане
Пользуясь выше приведенными формулами и табличными коэффициентами, можно построить эпюры нормальных напряжений σ z по вертикальной оси, проходящей через центр прямоугольного фундамента.
Для точек, расположенных под центром прямоугольной площади загружения (Рисунок 9, в) и под ее угловыми точками, решение плоской задачи сводится к выражению:
σ z = α р , (3.8)
где α - коэффициент, принимаемый по таблице 3.1;
р – равномерно распределенное давление .
Необходимо отметить, при определении углового напряжения параметр
m = z/b; при определении напряжений под центром прямоугольника m=2z/b.
Таблица 3. 1 - Коэффициенты уменьшения среднего дополнительного давления (коэффициент рассеивания напряжений по глубине) под подошвой фундамента, α
| m= =z/b | Круглый фунда- мент | Прямоугольный в плане фундамент при а : b | |||||||||
| 2,4 | 3,2 | ||||||||||
| 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | |
| 0,2 | 0,949 | 0,960 | 0,976 | 0,976 | 0,977 | 0,977 | 0,977 | 0,977 | 0,977 | 0,977 | 0,977 |
| 0.4 | 0,756 | 0,800 | 0,870 | 0,875 | 0,878 | 0,879 | 0,880 | 0,881 | 0,881 | 0,881 | 0,881 |
| 0,6 | 0,546 | 0,606 | 0,727 | 0,757 | 0,749 | 0,743 | 0,754 | 0,755 | 0,755 | 0,755 | |
| 0,8 | 0,390 | 0,449 | 0,593 | 0,612 | 0,627 | 0,630 | 0,636 | 0,639 | 0,640 | 0,641 | 0,642 |
| 1,0 | 0,284 | 0,334 | 0,480 | 0,505 | 0,526 | 0,529 | 0,540 | 0,545 | 0,547 | 0,549 | 0,550 |
| 1,2 | 0,214 | 0,257 | 0,392 | 0,419 | 0,443 | 0,449 | 0,462 | 0,470 | 0,474 | 0.476 | 0.477 |
| 1,4 | 0,165 | 0,201 | 0,323 | 0,350 | 0,376 | 0,383 | 0,400 | 0,410 | 0,414 | 0,418 | 0,420 |
| 1,6 | 0,130 | 0,160 | 0,267 | 0,294 | 0,322 | 0,329 | 0,348 | 0,360 | 0,365 | 0,370 | 0,374 |
| 1,8 | 0,106 | 0,130 | 0,224 | 0,250 | 0,278 | 0,285 | 0,305 | 0,320 | 0,326 | 0,332 | 0,330 |
| 2,0 | 0,087 | 0,108 | 0,189 | 0,214 | 0,237 | 0,241 | 0,270 | 0,285 | 0,0,293 | 0,301 | 0,304 |
| 2,2 | 0,073 | 0.090 | 0,163 | 0,185 | 0,213 | 0,218 | 0,239 | 0,256 | 0,264 | 0,273 | 0,280 |
| 2,4 | 0.062 | 0,077 | 0,141 | 0.161 | 0,185 | 0,192 | 0,213 | 0,230 | 0,238 | 0,250 | 0,258 |
| 2,6 | 0,053 | 0,066 | 0,123 | 0,141 | 0,164 | 0,170 | 0,191 | 0,208 | 0,216 | 0,229 | 0,239 |
| 2,8 | 0,046 | 0,0,058 | 0,108 | 0,124 | 0,145 | 0,152 | 0,172 | 0,189 | 0,197 | 0,212 | 0,228 |
| 3,0 | 0,040 | 0,051 | 0,095 | 0,110 | 0,130 | 0,136 | 0,155 | 0,172 | 0,180 | 0,194 | 0,208 |
| 3,2 | 0,036 | 0,045 | 0,085 | 0,098 | 0,116 | 0,122 | 0,0.141 | 0,158 | 0,165 | 0,178 | 0,190 |
| 3,4 | 0,032 | 0,040 | 0.076 | 0,088 | 0,105 | 0,110 | 0,128 | 0,144 | 0,151 | 0,161 | 0,184 |
| 3.6 | 0,028 | 0,036 | 0,068 | 0,080 | 0,095 | 0,100 | 0,117 | 0,133 | 0,140 | 0,153 | 0,175 |
| 3,8 | 0,024 | 0,032 | 0,068 | 0,072 | 0,086 | 0,091 | 0,107 | 0,123 | 0,130 | 0,144 | 0,166 |
| 4,0 | 0,022 | 0,029 | 0,056 | 0,066 | 0,080 | 0,084 | 0.095 | 0,113 | 0,121 | 0,135 | 0,158 |
| 5.0 | 0,015 | 0,019 | 0,037 | 0,044 | 0,053 | 0,056 | 0,067 | 0.79 | 0,089 | 0,103 | 0.126 |
| 7,0 | 0,008 | 0,010 | 0,019 | 0.023 | 0,029 | 0,032 | 0,039 | 0,045 | 0.051 | 0,062 | 0,091 |
| 10.0 | 0,004 | 0,005 | 0,010 | 0,012 | 0,014 | 0,016 | 0.019 | 0,023 | 0,027 | 0,033 | 0,064 |
Примечание. m – отношение сторон прямоугольной площади загружения; а – длинная ее сторона; b – короткая ее сторона; z- глубина, на которой определяется напряжение σ z . При использовании данных таблицы 3.1 напряжение под угловыми точками определяют по формуле (3.9):
σ z = 0,25 α р , (3.9)
В качестве примера на рисунке 10 в относительных координатах построены такие эпюры для разных случаев.
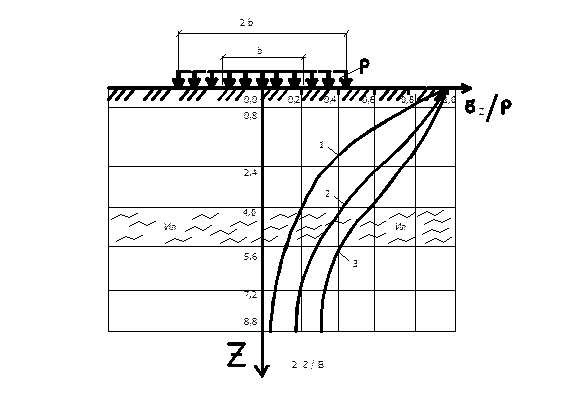
Рисунок 10 - Характер распределения напряжений σ z по оси
фундамента в зависимости от формы и площади его подошвы:
1 – для квадратного фундамента при l = b;
2 – для ленточного фундамента (l ≥ 10 b);
3 - то же, шириной 2b
Увеличение ширины, а следовательно и площади фундамента (кривая 3) приводит к более медленному затуханию напряжений с глубиной.
Это обстоятельство объяснимо из принципа суперпозиции. Если ленточный фундамент представить как ряд квадратных фундаментов, установленных вплотную друг к другу, можно с помощью метода угловых точек учесть дополнительное влияние нагрузки, действующей на соседние фундаменты.
Указанная закономерность имеет важное практическое значение. Если, например, в основании на некоторой глубине залегает слабый прослоек (ил на рисунке 10), то можно подобрать такую форму и площадь фундамента, чтобы напряжения на кровле этого прослойка были меньше его несущей способности.
В противном случае возможны чрезмерные осадки из-за выдавливания грунта слабого прослойка в стороны от оси фундамента.
Влияние неоднородности напластования грунтов. Приведенные выше решения справедливы для случая, когда основание сложено грунтами, близкими по деформационным показателям.

Рисунок 11 – Характер распределения напряжений σ zпо оси фундамента
при расположении подстилающего слоя на разной глубине:
1 – относительно однородное по сжимаемости основания;
2 – при наличии на соответствующих относительных глубинах z/b
практически несжимаемого слоя;
3 - то же, но значительно более слабого слоя, чем несущий слой грунта
Если же на некоторой глубине залегают существенно более жесткие (например, скальные) грунты, то возникает концентрация напряжений σ z по оси фундамента. Причем эффект концентрации напряжений тем больше, чем меньше относительная глубина залегания кровли этого слоя грунтов. Если же подстилающий слой грунта обладает значительно большей сжимаемостью, чем несущий, напротив, отмечается некоторое рассеивание (деконцентрация) напряжений σ z .
На рисунке 11 в качестве примера приведены также в относительных координатах эпюры напряжений σ zпо оси фундаментов.
Дата добавления: 2015-08-08; просмотров: 1649;
