Закон сохранения импульса. Движение тела с переменной массой.

Импульс (количество движения): .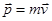

Второй закон (в формулировке самого Ньютона):

.

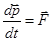1. Закон сохранения импульса для двух взаимодействующих тел (см. рис. 1 лекции 3)

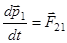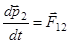, . По третьему закону Ньютона 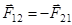. Отсюда

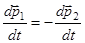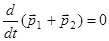, . Значит полный импульс двух взаимодействующих тел

сохраняется:

.

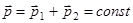2. Закон сохранения импульса для замкнутой системы из 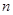взаимодействующих

материальных точек

Замкнутая система – на каждую из материальных точек действуют лишь силы со стороны

других точек, входящих в систему (нет внешних сил).

Уравнения второго закона Ньютона для 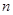точек:

,

,

. . . . . . . . . . . . . . . ,

.

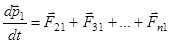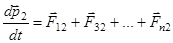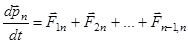Складывая эти уравнения и группируя слагаемые в правой части, получаем

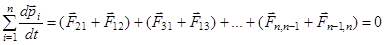(по третьему закону Ньютона).

Значит полный импульс системы 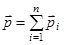сохраняется: , .

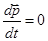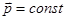3. Изменение полного импульса незамкнутой системы

В этом случае на каждую материальную точку действует внешняя сила 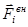. Проводя

аналогичное суммирование, получаем

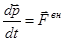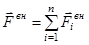, . (1)

Введем понятие центра масс системы материальных точек

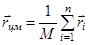, где 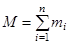- полная масса системы, 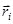- радиус-вектор 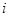-ой точки.

Тогда уравнение (1) можно записать в виде

.

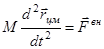4. Импульс силы. Движение тела с переменной массой.

Удобно использовать еще одну форму записи второго закона Ньютона

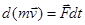. (2)

Величина 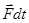называется импульсом силы.

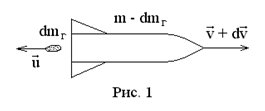Рассмотрим реактивное движение ракеты с учетом изменения ее массы из-за сгорания топлива. На рис. 1 представлены величины для ракеты и продуктов сгорания (индекс “г”) в момент времени 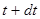. Пусть в момент 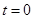масса ракеты равна 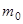, а скорость 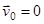. В момент 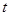скорость ракеты равна 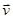, а масса - .

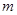Тогда уравнение (2) для ракеты можно представить в виде:

.

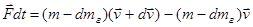Отсюда, с точностью до величин первого порядка малости, получим

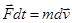. (3)

Уравнение (2) для продуктов сгорания:

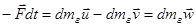, (4)

где 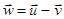- скорость продуктов сгорания относительно ракеты. Так как 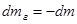, то из уравнений (3), (4) следует, что

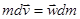или .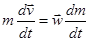

Последнее уравнение называется уравнением Мещерского. В проекции на направление движения ракеты получим

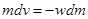или .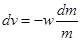

После интегрирования приходим к формуле Циолковского

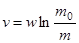. (5)

Эта формула сыграла очень важную роль в истории космонавтики. Она позволяет оценить количество топлива необходимого для космических полетов. Можно, например, провести такую оценку для полета за пределы солнечной системы. Минимальное значение скорости, которую должна в этом случае развить ракета равно 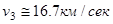(третья космическая скорость). Современное химическое топливо дает значение 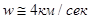. Тогда из формулы (5) получим

.

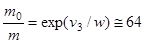Для полета туда и обратно необходимо значение 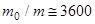. Однако, скорости 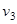недостаточно для полета к другим звездам за разумные промежутки времени. От ближайшей к нам звезды α-Центавра свет доходит до Земли за 4 года. Следовательно, ракета должна развивать скорость сравнимую со скоростью света. С учетом прогресса в области разработки новых видов топлива возьмем завышенное значение 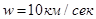. Тогда при 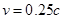получим

.

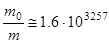Нереальность такой величины очевидна по той причине, что масса всей нашей Галактики составляет ≈ 10⁴¹ кг. Один из гипотетических вариантов осуществления межзвездных полетов предполагает использование фотонных ракетных двигателей со значением 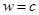. Однако, до практической реализации таких идей еще далеко.