ЛЕКЦИЯ 6. Упругие и неупругие столкновения.

Упругие и неупругие столкновения.

Рассмотрим столкновение двух шаров, скорости которых направлены вдоль линии, соеди-няющей их центры (центральный удар). Будем считать систему шаров замкнутой и полную энергию шаров до и после удара одинаковой. Такой удар называется абсолютно упругим. Запишем закон сохранения импульса в проекции на ось 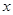, проходящую через центры шаров, и закон сохранения энергии:

,

.

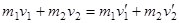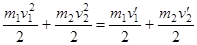Считая проекции скоростей 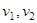до удара заданными, из этой системы уравнений находим проекции скоростей шаров 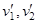после удара

, .

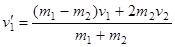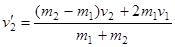Рассмотрим различные частные случаи.

1) Массы шаров одинаковы: 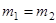. В этом случае 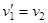, , 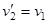то есть шары обмениваются скоростями.

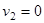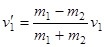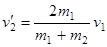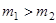2) Второй шар покоился до удара: . Тогда , . При и 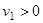шары после удара движутся в одну сторону: 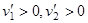. При 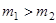более легкий шар отражается в противоположном направлении, то есть 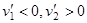. При 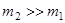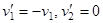(отражение от неподвижной стенки).

Перейдем к рассмотрению неупругих ударов. В этом случае часть кинетической энергии шаров переходит в тепловую энергию :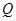

.

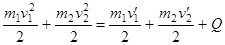Если величина 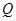неизвестна, то решить задачу о столкновении в общем случае невоз-можно. Однако, есть один очень важный частный случай, когда задача решается до конца. Абсолютно упругий удар – тела после удара движутся с одинаковой скоростью (“слипаются”).

В этом случае закон сохранения импульса принимает вид:

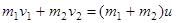. Отсюда .

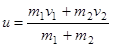Из закона сохранения полной энергии с учетом количества тепла находим

.

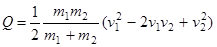Удобно записать это выражение в следующем ви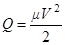де:

, где 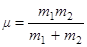- приведенная масса , 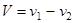- относительная скорость

сталкивающихся тел.

Нецентральный удар

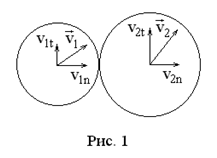Разложим скорости шаров в момент столкновения на нормальную и тангенциальную составляющие по отношению к плоскости касания шаров. В этом случае законы сохранения импульса и энергии для абсолютно упругого удара можно представить в следующем виде

,

,

.

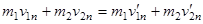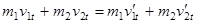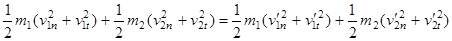Итак, имеем три уравнения для четырех неизвестных. Поэтому задача не имеет однознач-ного решения. Такое решение существует в случае идеально гладких шаров (нет сил тре-ния), когда 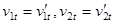. При этом одно уравнение исключается и остается две неизвестные величины.

Описание столкновений в системе центра масс

Центр масс двух сталкивающихся тел движется со скоростью

.

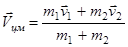Если система тел является замкнутой, то 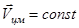. Систему отсчета, в которой заданы скорости 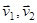будем называть лабораторной системой отсчета. В ней мы рассматриваем процесс столкновения тел. Оказывается, что более удобно с вычислительной точки зрения изучать такой процесс в системе центра масс двух тел, движущейся со скоростью 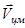. Будем обозначать величины в системе центра масс индексом “0”. В силу того, что центр масс в такой системе неподвижен, для импульсов до и после столкновения имеют место соотношения

, .

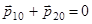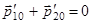Тогда с помощью закона сохранения энергии

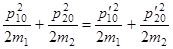
легко получить, что

, .

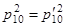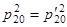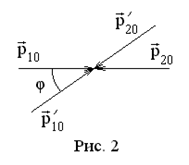Это означает, что в системе центра масс импульсы тел до столкновения и после столкновения противоположно направлены и имеют одинаковую абсолютную величину (см. рис. 2). В результате взаимодействия тел происходит поворот импульсов в системе центра масс на некоторый угол 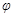. Значение этого угла можно найти только если известны силы взаимодействия между телами. Рассмотрим важный частный случай, когда второе тело в лабораторной системе покоится до столкновения 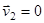. Тогда

, , , .

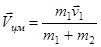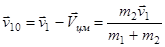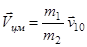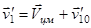Эти соотношения приводят к удобному графическому приему, представленному на рис. 3. Пусть 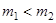. Тогда 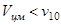. Угол 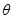между вектором скорости налетающей частицы 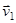до столкновения и вектором скорости 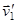после столкновения называется углом рассеяния. Рассмотренный случай столкновения соответствует, в частности, опытам Резерфорда по рассеянию 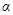- частиц на тяжелых ядрах. Эти опыты привели в дальнейшем к созданию атомной физики. В случае, когда 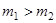(налетающая частица тяжелее покоящегося), 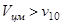и точка 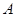будет лежать вне окружности. При этом угол рассеяния будет ограничен некоторым значением 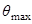для которого отрезок 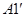является касательной к окружности и 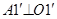. Отсюда легко получить

.

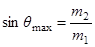Система центра масс обычно используется для расчета движения двух взаимодействующих тел (задача двух тел).