ЛЕКЦИЯ 9. Общий случай вращательного движения твердого тела

Общий случай вращательного движения твердого тела. Гироскопические явления.

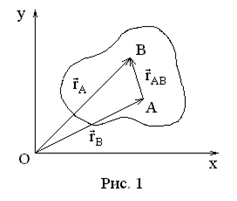Рассмотрим движение плоского твердого тела в его собственной плоскости . Выберем в нем две произвольные точки и . Так как тело является твердым, то при его движении

.

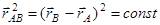Продифференцируем это соотношение по времени

.

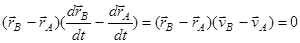Пусть в данный момент времени 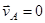. Тогда для всех точек 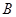имеем 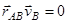. Это означает, что скорости перпендикулярны соответствующим радиусам. Следовательно, можно говорить о вращении в данный момент времени вокруг оси, проходящей через точку .

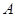Мгновенная ось вращения - прямая, проходящая через точки тела, скорости которых в данный момент времени равны нулю.

Например, для цилиндра, катящегося по плоскости, мгновенная ось вращения проходит через точки соприкосновения цилиндра с плоскостью (лекция 2).

Имеет место важная теорема, относящаяся к движению тела с одной неподвижной точкой. Мы приведем ее без доказательства.

Теорема Эйлера

Твердое тело, имеющее одну неподвижную точку, может быть переведено из произвольного положения в другое произвольное положение путем поворота вокруг некоторой оси, прохо-дящей через эту точку.

Произвольное движение твердого тела.

Его можно представить как совокупность поступательного движения всего тела со ско-ростью 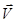его некоторой точки 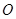(основная точка) и вращательного с угловой скоростью 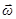вокруг мгновенной оси, проходящей через эту точку. При этом угловая скорость 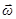не зависит от выбора основной точки .

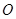Выберем в качестве основной точки центр масс тела. Пусть 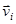- скорость вращательного движения 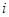- го элемента тела относительно мгновенной оси. Тогда полную кинетическую энергию тела можно представить в виде

.

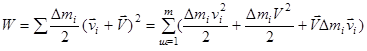Последнее слагаемое в правой части равенства при суммировании дает нуль, так как ось проходит через центр масс. Тогда приходим к выражению (теорема Кёнига)

.

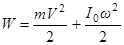Получим одно важное соотношение между энергией вращательного движения 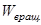и моментом импульса тела 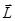. Оно понадобится нам в дальнейшем. Можно легко убедиться в том, что скорость вращения 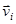и угловая скорость 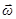связаны соотношением 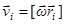. Тогда

.

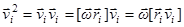Последнее из равенств доказывается в векторной алгебре. В этом случае для 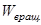получим

.

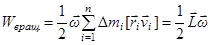В частном случае вращения осесимметричного тела вокруг его оси 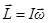и .

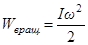Гироскоп – быстровращающееся осесимметричное тело, ось вращения которого может изменять свое направление в пространстве.

Движение гироскопа описывается основным законом вращательного движения в общем виде

.

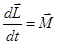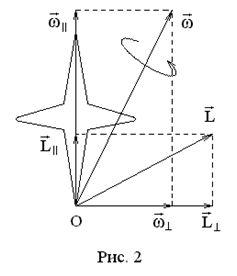При этом ось вращения и момент импульса не обяза-тельно совпадают с осью гироскопа. Рассмотрим движение гироскопа с одной неподвижной точкой (т. О на рис. 2). Тогда по теореме Эйлера в каждый момент времени происходит вращение вокруг мгновенной оси проходящей через т. О. Разложим вектора 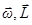на составляющие вдоль оси гироскопа и перпендикуляр-ные к оси гироскопа (см. рис. 2). Физический смысл суммы векторов 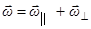состоит в том, что при этом тело вращается вокруг собственной оси с угловой скоростью 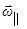, а сама эта ось вращается вокруг оси перпендикулярной к собственной со скоростью .

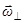Момент импульса гироскопа можно представить в виде

,

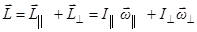где 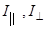- моменты инерции гироскопа относительно соответствующих осей. Тогда

.

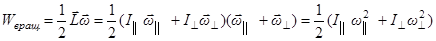Свободный гироскоп ( ).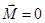

В этом случае выполняются законы сохранения момента импульса и энергии

,

.

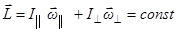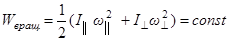Отсюда следует, что при движении свободного гироскопа значения 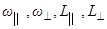остаются постоянными. Это означает, что имеет место так называемая свободная регулярная прецессия: в каждый момент времени движение свободного гироскопа есть вращение вокруг мгновенной оси, проходящей через неподвижную точку опоры; направление вектора 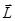неизменно в пространстве, а ось гироскопа и мгновенная ось вращения вращаются вокруг 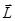с постоянной угловой скоростью .

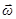Вынужденная прецессия гироскопа

При кратковременном воздействии на гироскоп 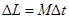мало по сравнению с 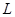в силу большой угловой скорости вращения вокруг собственной оси. То есть имеет место устойчи-вость движения свободного гироскопа. Это находит применение в многочисленных приложениях (автопилоты, гирокомпасы, движение мотоциклов и велосипедов и т. д.).

Совсем по-другому ведет себя несвободный гироскоп, находящийся под действием постоян-ной силы.

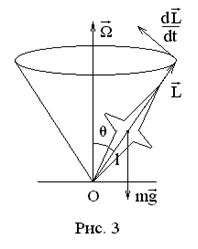
Рассмотрим движение гироскопа с одной неподвижной точкой в поле тяжести (рис. 3).

Будем считать, что 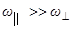(приближенная теория гироскопа). В этом случае момент импульса гироскопа направлен вдоль его оси и равен 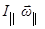. Основной закон вращательного движения имеет вид:

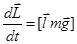. С другой стороны можно считать, что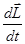

является “скоростью движения” конца вектора 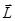. Тогда по аналогии с формулой 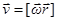можно записать, что

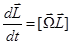. Отсюда 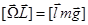или 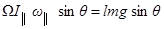. Отсюда находим

.

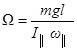Ось гироскопа в этом случае описывает конус, совершая вращение с угловой скоростью .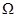

Такое движение называется вынужденной прецессией гироскопа под действием внешней силы. Гироскопические явления играют важную роль в самых разнообразных физических системах, от механических до атомных.