Ускорение точки при естественном способе задания движения
Известна зависимость дуговой координаты S от времени 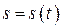 . Скорость точки определяется формулой:
. Скорость точки определяется формулой:
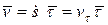 .
.
Найдём ускорение, продифференцировав это соотношение по времени. Учтём при этом, что единичный вектор касательной 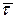 меняет направление при движении точки, и он может быть рассмотрен как сложная векторная функция
меняет направление при движении точки, и он может быть рассмотрен как сложная векторная функция 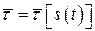 . Тогда
. Тогда
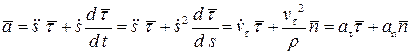
где 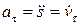 — называется касательным (тангенциальным) ускорением,
— называется касательным (тангенциальным) ускорением, 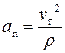 — называется нормальным ускорением.
— называется нормальным ускорением.
Т. к. 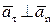 , модуль ускорения можно найти по теореме Пифагора:
, модуль ускорения можно найти по теореме Пифагора:
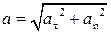
Дата добавления: 2015-08-08; просмотров: 688;
