Метод сечений. Напряжение
Знать метод сечений, внутренние силовые факторы, составляющие напряжений.
Уметь определять виды нагружений и внутренние силовые факторы в поперечных сечениях.
Для расчетов деталей машин и сооружений на прочность необходимо знать внутренние силы упругости, возникающие в результате действия приложенных к деталям внешних сил.
В теоретической механике мы имели дело с неизменяемыми системами; в сопротивлении материалов рассматриваются изменяемые (деформируемые) системы материальных точек.
Метод сечений заключается в том, что тело мысленно разрезается плоскостью на две части, любая из которых отбрасывается и взамен нее к сечению оставшейся части прикладываются внутренние силы, действовавшие до разреза; оставленная часть рассматривается как самостоятельное тело, находящееся в равновесии под действием внешних и приложенных к сечению внутренних сил.
Очевидно, что, согласно третьему закону Ньютона (аксиома взаимодействия), внутренние силы, действующие в сечении оставшейся и отброшенной частей тела, равны по модулю, но противоположны по направлению. Таким образом, рассматривая равновесие любой из двух частей рассеченного тела, мы получим одно и то же значение внутренних сил, однако выгоднее рассматривать ту часть тела, для которой уравнения равновесия проще.
В соответствии с принятым допущением о непрерывности материала тела мы можем утверждать, что внутренние силы, возникающие в теле, представляют собой силы, равномерно или неравномерно распределенные по сечению.
Применяя к оставленной части тела условия равновесия, мы не сможем найти закон распределения внутренних сил по сечению, но сможем определить статические эквиваленты этих сил.
Так как основным расчетным объектом в сопротивлении материалов является брус и чаще всего нас будут интересовать внутренние силы в его поперечном сечении, то рассмотрим, каковы будут статические эквиваленты внутренних сил в поперечном сечении бруса.
Рассечем брус (рис. 4.3) поперечным сечением а —а ирассмотрим равновесие его левой части.
Если внешние силы, действующие на брус, лежат в одной плоскости, то в общем случае статическим эквивалентом внутренних сил, действующих в сечении а —а, будут главный вектор Fгл приложенный в центре
рис.4.6 тяжести сечения, и главный момент Ми, уравновешивающие плоскую систему внешних сил, приложенных к оставленной части бруса.
Разложим главный вектор на составляющую N, направленную вдоль оси бруса, и составляющую Q, перпендикулярную этой оси, т. е. лежащую в плоскости поперечного сечения.
Эти составляющие главного вектора вместе с главным моментом назовем внутренними силовыми факторами, действующими в сечении бруса. Составляющую N назовем продольной силой, составляющую Q — поперечной силой, пару сил МИ — изгибающим моментом.
Для определения указанных трех внутренних силовых
факторов статика дает три уравнения равновесия оставленной части бруса, а именно:
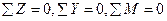
(ось z всегда направляем по оси бруса).
Если внешние силы, действующие на брус, не лежат в одной плоскости, т. е. представляют собой пространственную систему сил, то в общем случае в поперечном сечении бруса возникают шесть внутренних силовых факторов (рис. 4.7), для определения которых статика дает шесть уравнений равновесия оставленной части бруса, а именно:
Шесть внутренних силовых факторов, возникающих в поперечном сечении бруса в самом общем случае, носят следующие названия: Сила N — продольная сила вызывает появление нормального напряжения, Qx, Qy — поперечные силы вызывет касательно енапряжение, Мк — крутящий момент, Мu x,вызывет сдвиг сечения вокруг продольной оси, поэтому появляются касательные напряжения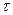 
, Мu у — изгибающие моменты.
Главный момент тоже принято представлять в виде моментов пар в трех плоских проекции:
При разных деформациях в поперечном сечении бруж возникают различные внутренние силовые факторы. Рассмотрим частные случаи:
1. В сечении возникает только продольная сила N. В этом случае это деформация растяжения (если сила TV направлена от сечения) или деформация сжатия (если сила N направлена к сечению).
2. В сечении возникает только поперечная сила Q. В этом случае это деформация сдвига.
-3. В сечении возникает только крутящий
рис.4.7 момент Мк. В этом случае это деформация кручения.
4. В сечении возникает только изгибающий момент Ми. В этом случае это деформация чистого изгиба. Если в сечении одновременно возникает
изгибающий момент Ми и поперечная сила Q, то изгиб называют поперечным.
5. Если в сечении одновременно возникает несколько внутренних силовых факторов (например, изгибающий и крутящий моменты или изгибающий момент и продольная сила), то в этих случаях имеет место сочетание основных деформаций.
Наряду с понятием деформации одним из основных понятий сопротивления материалов является напряжение. Напряжение характеризует интенсивность внутренних сил, действующи в сечении.
Рассмотрим какой-либо произвольно нагруженный брус и применим к нему метод сечений (рис. 4.8). Выделим в сечении бесконечно малый элемент площади dA (что мы имеем право делать, так как считаем материал непрерывным). Ввиду малости этого элемента можно считать, что в его пределах внутренние силы, приложенные в различных точках, одинаковы по модулю и направлению и, следовательно, представляют собой систему параллельных сил. Равнодействующую этой системы обозначим dF. Разделив dF на площадь элементарной площадки dА, определим интенсивность внутренних сил, т. е. напряжение р в точках элементарной площадки dА:
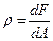
Таким образом, напряжение есть внутренняя сила, отнесенная к единице площади сечения.
Напряжение есть величина векторная. Единица напряжения:
Поскольку эта единица напряжения очень мала, то мы будем применять более крупную кратную единицу, а именно мегапаскаль (Мпа):
1 Мпа=106 Па=1 Н/мм2.
Числовые значения напряжения, выраженного в Мпа и Н/мм2, совпадают.
Разложим вектор напряжения р на две составляющие: 
— перпендикулярную плоскости сечения и 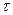— лежащую в плоскости сечения (рис. 4.8). Эти составляющие назовем так: — нормальное напряжение, 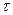— касательное напряжение.
рис.4.8
Так как угол между нормальным и касательным напряжениями всегда равен 90°, то модуль полного напряжения р определится по формуле
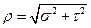
Если вектор пространственный, то его раскладывают на три составляющие:
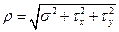
Разложение полного напряжения на нормальное и касательное имеет вполне определенный физический смысл. Как мы убедимся в дальнейшем, в поперечном сечении бруса при растяжении, сжатии и чистом изгибе действуют только нормальные напряжения, а при сдвиге и кручении—только касательные напряжения.
В заключение настоящей главы рассмотрим гипотезу, которая носит название принципа независимости действия сил и формулируется так: при действии на тело нескольких нагрузок внутренние силы, напряжения, перемещения и деформации в любом месте могут быть определены как сумма этих величин, найденных от каждой нагрузки в отдельности.
Пользуясь принципом независимости действия сил, мы, начав с изучения простейших основных деформаций, когда в поперечных сечениях бруса действуют только нормальные или только касательные напряжения, в дальнейшем перейдем к изучению более сложных основных деформаций, когда в поперечном сечении действуют и те и другие напряжения, а затем рассмотрим случаи сочетания основных деформаций, что иногда называют сложным сопротивлением.
Заметим, что принцип независимости действия сил применим только для конструкций, деформации которых малы по сравнению с размерами и пропорциональны действующим нагрузкам
Дата добавления: 2015-08-08; просмотров: 2066;