Закон де Моргана
Этот закон широко используется при минимизации переключательных функций и выражается формулами:
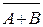 ≡
≡ 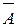 &
& 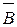
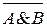 ≡
≡ 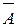 +
+ 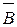
отрицание любого сложного высказывания эквивалентно сложному высказыванию, в котором исходные знаки дизъюнкции заменены знаками конъюнкции, знаки конъюнкции – знаками дизъюнкции, и все составляющие его аргументы – их отрицаниями.
Пример 1: высказывание А – любое,
высказывание В= 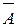 .
.
Тогда 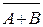 =
=  =
= 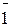 = 0, (под знаком отрицания – закон исключенного третьего)
= 0, (под знаком отрицания – закон исключенного третьего)
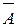 &
& 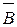 =
= 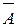 &
& 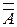 =
= 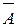 &A = 0.
&A = 0.
Пример 2: высказывание А=”Число заканчивается на 0”,
высказывание В=”Число заканчивается на 5”.
Тогда высказывание A + B =”Число заканчивается на 0 ИЛИ число заканчивается на 5”.
Это признак делимости числа на 5.
Тогда признак неделимости числа на 5 формулируется так 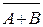 =
= 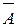 &
& 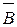 =”Число НЕ заканчивается на 0 И число НЕ заканчивается на 5”.
=”Число НЕ заканчивается на 0 И число НЕ заканчивается на 5”.
Кроме законов, выраженных тавтологиями, в алгебре логики рассматриваются законы (теоремы), позволяющие упростить или преобразовать сложные логические выражения.
К таким законам относятся следующие:
- коммутативный (переместительный) закон:
A + B ≡ B + A
A & B ≡ B & A
- сочетательный закон:
A + (B + C) ≡ (A + B) + C
A & (B & C) ≡ (A & B) & C
- распределительный закон:
A & (B + C) ≡ A & B + A & C
A + B & C ≡ (A + B) & (A + C)
- закон поглощения:
A + A&B = A&(1 + B) = A
A&(A + B) = A&A + A&B = A + A&B = A&(1 + B) = A
- закон склеивания:
A&B + A& 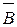 = A&(B +
= A&(B + 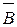 ) = A&1 = A
) = A&1 = A
Кроме этих законов, в алгебре логики рассматриваются следующие соотношения:
A + 0 = A
A + 1 = 1
A & 0 = 0
A & 1 = A
A + A = A
A & A = A
Любую формулу алгебры логики можно представить таблицей истинности, перебрав все значения ее аргументов:
F = A& 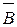 + A&B
+ A&B
| A | B | F |
Любую таблицу истинности можно представить формулой алгебры логики:
| A | B | F |
Оставляем в таблице только те строки, в которых значение функции истинно:
| A | B | F |
Составляем сумму произведений аргументов, причем если значение аргумента ложно, то записываем его с отрицанием:
F = 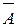 &
& 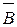 +A&
+A& 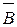
Далее можно упростить эту формулу:
F = 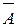 &
& 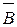 +A&
+A& 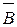 =
= 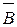 &(
&( 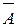 + A) =
+ A) = 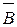 & 1 =
& 1 = 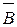
Приложение 2
Дата добавления: 2015-08-08; просмотров: 907;
