Упражнение 5. Решение системы линейных уравнений Методом Крамера
Дана линейная система 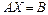 , где
, где 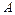 – матрица коэффициентов,
– матрица коэффициентов, 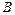 – столбец (вектор) свободных членов,
– столбец (вектор) свободных членов, 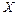 – столбец (вектор) неизвестных.
– столбец (вектор) неизвестных.
По методу Крамера 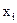 вычисляется по формуле
вычисляется по формуле 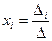 , где
, где 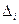 - определители матрицы
- определители матрицы 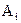 ,
, 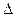 - определитель исходной матрицы т.е матрицы А.
- определитель исходной матрицы т.е матрицы А. 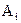 получается из матрицы A заменой i-того столбца столбцом "b"-свободных членов. Это определяет метод реализации алгоритма в Excel.
получается из матрицы A заменой i-того столбца столбцом "b"-свободных членов. Это определяет метод реализации алгоритма в Excel.
Например, нужно решить систему линейных уравнений с 3 неизвестными, с коэффициентами 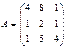 и с правой частью
и с правой частью 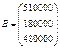 .
.
- Вводим матрицы A, b, затем копируем матрицу A три раза (начальная заготовка для матрицы
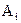 ) рис.1.
) рис.1.
| B | C | D | E | F | G | H | I | J | |
| 510 000 | |||||||||
| A | Det(A)= | В | 180 000 | ||||||
| 480 000 | |||||||||
| A1 | Det(A1)= | X1= | |||||||
| A2 | Det(A2)= | X2= | |||||||
| A3 | Det(A3)= | X3= | |||||||
Рис. 1
2. Затем копируем столбец b и вставляем его в А1 в 1 столбец, в А2 во 2 столбец, в А3 - в 3 столбец
3.Вычислите определители полученных матриц в ячейки Н7, Н11, Н15.
4.После определения определителей матриц А1, А2, А3 легко можно получить Х1 по формуле 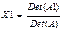 , и так для Х2, Х3
, и так для Х2, Х3
Задания для самостоятельной работы:
1. Решить системы линейных уравнений а) Методом Крамера
2. Вычислите б) квадратичную форму 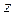 .
.
Таблица 1.
| № | Задание № 1 | Матрица 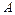
| 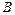
| 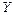
| № | Задание №1 | Матрица 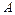
| 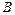
| 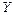
| |
а) 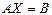 б)
б) 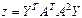
| 
| 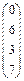
| 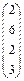
| а)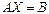 б)
б)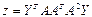
| 
| 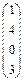
| 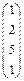
| |||
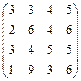
а) 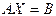 б)
б)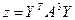
| 
| 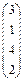
| 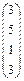
| а)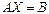 б)
б)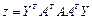
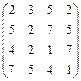
| 
| 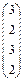
| 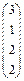
| |||
а)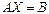 бв)
бв)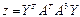
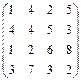
| 
| 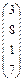
| 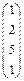
|
3.Найдите значение сложных выражений 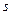 , где а, x, y – вектор из n компонентов,
, где а, x, y – вектор из n компонентов, 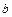 и
и 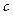 – матрица размерности
– матрица размерности 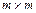 .
.
Таблица 2.
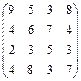
| № | Выражения 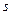
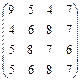
| Вектор а, x, y | Матрица 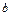 , , 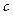
|
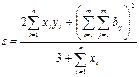
| 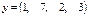 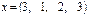
| 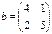
| |
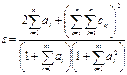
| 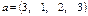
| 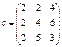
| |
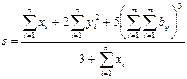
| 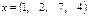
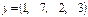
| 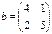
| |
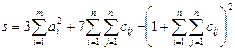
| 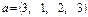
| 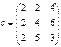
| |
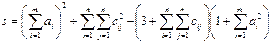
| 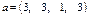
| 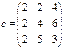
|
Контрольные вопросы:
- Что значит транспонировать матрицу?
- С помощью каких функций сумм вычисляются сложные выражения?
- В чем заключается метод Крамера?
- При каком условии система линейных уравнений имеет решение?
- Что выполняет функция СУММКВ?
Дата добавления: 2015-08-08; просмотров: 831;
