Лабораторная работа №14
Тема: «Поиск решения и решение оптимизационных задач. Линейная оптимизационная задача. Планирования производства красок»
Цель работы:сформировать умение решать линейные оптимизационные задачи.
Основные понятия:
Поиск решения (Solver) – это единый, мощный инструмент решения оптимизационных задач.
Упражнение 1. Задача об оптимальном производстве красок. Небольшая фабрика выпускает два типа красок: для внутренних (I) и наружных работ (E). Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта А и В. Максимально возможные суточные запасы этих продуктов составляет 6 т и 8 т соответственно. Расходы А и В на 1 т соответствующих красок приведены в таблице 1.
Таблица 1.
| Исходный продукт | Расход исходных продуктов (в тоннах) на тонну краски | Максимально возможный запас, т | |
| краска Е | краска I | ||
| А | |||
| В |
Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает спроса на краску E более чем на 1 т. Кроме того, установлено, что спрос на краску I никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3 000 руб. для краски E и 2 000 руб. для краски I . Какое количество краски каждого вида фабрика, чтобы доход от реализации продукции был максимальным?
1.1. Для решения этой задачи необходимо сначала построить математическую модель:
- Для определения каких величин строится модель? Что является переменными модели?
- В чем состоит цель, для достижения которой из множества всех допустимых значений переменных выбираются оптимальные?
- каким ограничениям должны удовлетворять неизвестные?
В нашем случае фабрике необходимо спланировать объем производства красок так, чтобы максимизировать прибыль. Поэтому переменными являются
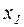 – суточный объем производства краски I;
– суточный объем производства краски I; 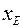 – суточный объем производства краски E.
– суточный объем производства краски E.
Суммарная суточная прибыль от производства хI краски Iи хЕ краски E равна 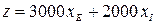 .
.
Целью фабрики является определение среди всех допустимых значений 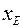 и
и 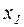 таких, которые максимизируют суммарную прибыль, т.е. целевую функцию
таких, которые максимизируют суммарную прибыль, т.е. целевую функцию 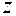 . Перейдем к ограничениям, которые налагаются на
. Перейдем к ограничениям, которые налагаются на 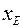 и
и 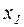 . Объем производства красок не может быть отрицательным, следовательно,
. Объем производства красок не может быть отрицательным, следовательно, 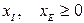 . Расход исходного продукта для производства обоих видов красок не может превосходить максимально возможный запас данного исходного продукта. Следовательно:
. Расход исходного продукта для производства обоих видов красок не может превосходить максимально возможный запас данного исходного продукта. Следовательно: 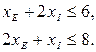
Кроме того ограничения на величину спроса на краски таковы: 
Таким образом. Математическая модель данной задачи имеет следующий вид:
Максимизировать 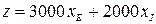 при следующих ограничениях:
при следующих ограничениях:

Заметим, что данная модель является линейной, т.к. целевая функция и ограничения линейно зависят от переменных.
1.2. Введите данные как в таблице 2. Отведем ячейки А3 и В3 под значения переменных 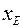 и
и 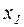 .
.
Таблица 2.
 1.3. Выберите команду Сервис/Поиск решения. Если отсутствует команда Поиск решения, то для ее установки необходимо выполнить команду Сервис/Надстройки/Поиск решения. В открывшемся диалоговом окне, в поле Установить целевую ячейку сделайте ссылку на ячейку С4, включите Равной Максимальному значению, введите в полеЗначению 0, в поле Изменяя ячейки укажите диапазон ячеек А3:В3. Переходите в поле Ограничения и нажмите кнопку Добавить и в следующем диалоговом окне Добавления ограничениявведите ограничения:
1.3. Выберите команду Сервис/Поиск решения. Если отсутствует команда Поиск решения, то для ее установки необходимо выполнить команду Сервис/Надстройки/Поиск решения. В открывшемся диалоговом окне, в поле Установить целевую ячейку сделайте ссылку на ячейку С4, включите Равной Максимальному значению, введите в полеЗначению 0, в поле Изменяя ячейки укажите диапазон ячеек А3:В3. Переходите в поле Ограничения и нажмите кнопку Добавить и в следующем диалоговом окне Добавления ограничениявведите ограничения:

1.3. Теперь нажмите кнопку Параметры в диалоговом окне Поиск решения, для того чтобы проверить, какие параметры заданы для поиска решений.
1.4. Запишите в тетради условие задачи, алгоритм нахождения решений и сделайте соответствующий вывод.
Задания для самостоятельной работы:
Вариант 1. Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линий 75 изделий. На радиоприемник первой модели расходуется 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй модели равна $30 и $20 соответственно. Определить оптимальный суточный объем производства первой и второй модели.
Вариант 2. Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Время использования этих станков для производства данных изделий ограничено 10 ч в сутки. Найти оптимальный объем производства изделий каждого вида.
| Изделие | Время обработки одного изделия, мин | Удельная прибыль | ||
| Станок 1 | Станок 2 | Станок 3 | ||
Вариант 3.Фирма имеет возможность рекламировать свою продукцию, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.
Вариант 4.Автозавод выпускает автомобили четырех видов: W,X,Y,Z (Хат, Седан, Джип, Вагон). Ежемесячно он может выпускать не более 1000 автомобилей (при этом каждого типа – не меньше 100). В течение месяца 1000 работников завода работают по 150 часов каждый. Завод может израсходовать за месяц не более 900 тонн стали.
| Модель продукций | Затраты стали | Затраты времени | Прибыль с единицы продукта |
| W (Хат) | 0,76 | ||
| X (Седан) | 1,00 | ||
| Y (Джип) | 0,72 | ||
| Z (Вагон) | 1,50 |
Контрольные вопросы:
- Какое средство Excel используется для решения линейных оптимизационных задач?
- Каким образом записываются ограничения?
- Что такое целевая функция?
- Что такое математическая модель?
- Как вы понимаете переменные модели?
Дата добавления: 2015-08-08; просмотров: 1215;
