Технология работы.
1. Переименуйте Лист1 на Задание 3
2. Вычислим A-1 описанным ранее методом. Так как Ax=b , то x=A-1 b. Для определения х необходимо перемножить полученную обратную матрицу A-1 и столбец свободных членов . Алгоритм представлен на рис. 1 а результаты решения на рис. 2
| B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | |
| =МОБР(C2:E4) | =МУМНОЖ(K2:M4;H2:H4) | |||||||||||||||
| A | B | A-1 | X | |||||||||||||
Рис.1
| B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | |
| 510 000 | -0,3333 | -0,667 | ||||||||||||||
| A | B | 180 000 | A-1 | 0,33333 | -1,6667 | 0,333 | X | |||||||||
| 480 000 | -0,3333 | 1,3333 | ||||||||||||||
Задания для самостоятельной работы:
1. Сложите массивы А+В=...
2. Вычислите произведение матриц А*В=...
3. Найдите обратную матрицу к матрице (А+В). Проверьте результат, вычислив произведение исходной матрицы и обратной к ней.
4. Решите систему линейных уравнений методом обратной матрицы.
| № вар | Задание 1-3. | Задание 4 |
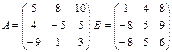
| 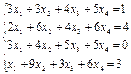
| |

| 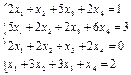
| |
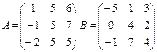
| 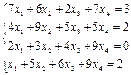
| |

| 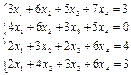
| |
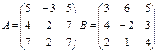
| 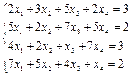
|
Контрольные вопросы:
- Что представляет с собой массив?
- С помощью каких клавиш обеспечивается ввод формул во все элементы массива?
- Что выполняет функция МОПРЕД?
- Какая функция выполняет умножение массивов?
- Как решить систему линейных уравнений с помощью обратной матрицы?
Дата добавления: 2015-08-08; просмотров: 713;
