Квантовые числа. Строение электронных оболочек.
Теория Бора не была ни последовательно классической, ни последовательно квантовой теорией. Недостатки теории Бора были устранены путем создания новой квантовой теории, в которой поведение и движение микрочастиц подчиняется своим законам. Это было осуществлено при создании квантовой механики, поэтому теория Бора положило начало развитию квантовой теории строения атома.
В соответствии с этой теорией состояние электрона в атоме характеризуется четырьмя квантовыми числами. Первое их квантовых чисел – главное квантовое число: n=1; 2; 3, … Оно определяет уровни энергии электрона в атоме. Второе квантовое число – орбитальное квантовое число l, которое при данном n может принимать значения 0, 1, 2, ..., n–1 . Это число определяет орбитальный момент импульса 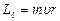 электрона относительно ядра. Третье квантовое число – магнитное квантовое число
электрона относительно ядра. Третье квантовое число – магнитное квантовое число 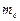 , которое при данном lпринимает значения 0; ±1; ±2,…, ±l; всего 2l +1 значений. Это число определяет проекции орбитального момента импульса электрона на некоторое произвольно выбранное направление Z. Четвертое квантовое число – спиновое квантовое числоms. Оно может принимать только два значения
, которое при данном lпринимает значения 0; ±1; ±2,…, ±l; всего 2l +1 значений. Это число определяет проекции орбитального момента импульса электрона на некоторое произвольно выбранное направление Z. Четвертое квантовое число – спиновое квантовое числоms. Оно может принимать только два значения 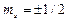 и характеризует возможные значения проекции на ось Z спина (собственного механического момента импульса)
и характеризует возможные значения проекции на ось Z спина (собственного механического момента импульса) 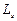 электрона.
электрона.
В 1924 г. швейцарский физик Паули сформулировал принцип, согласно которому: в любом атоме не может быть двух электронов, находящихся в двух одинаковых стационарных состояниях, определяемых набором четырех квантовых чисел – главного n; орбитального 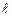 ; магнитного m и спинового ms. Принципу Паули, кроме электронов подчиняются другие частицы, имеющие полуцелый спин (в единицах
; магнитного m и спинового ms. Принципу Паули, кроме электронов подчиняются другие частицы, имеющие полуцелый спин (в единицах 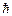 ).
).
Для электронов в атоме принцип Паули записывается таким образом: 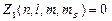 или 1, где
или 1, где 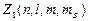 –число электронов в состоянии, характеризуемом данным набором квантовых чисел. Максимальное число электронов, находящихся в состояниях, описываемых набором трех квантовых чисел n;
–число электронов в состоянии, характеризуемом данным набором квантовых чисел. Максимальное число электронов, находящихся в состояниях, описываемых набором трех квантовых чисел n; 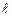 и m и отличающихся только ориентацией спинов электронов, равно
и m и отличающихся только ориентацией спинов электронов, равно 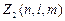 =2, т.к. ms принимает два значения, т.е. ±1/2. Максимальное число
=2, т.к. ms принимает два значения, т.е. ±1/2. Максимальное число 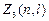 электронов, находящихся в состояниях, описываемых двумя квантовыми числами n и l:
электронов, находящихся в состояниях, описываемых двумя квантовыми числами n и l: 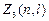 =2(2l+1), т. к. m принимает 2l + 1 значений,
=2(2l+1), т. к. m принимает 2l + 1 значений,
Определим максимальное число электронов с определенным l.
Электроны с l=0 называются s-электронами: 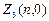 = 2(2×0+1)=2.
= 2(2×0+1)=2.
Электроны с l=1 называются р-электронами:  =2(2×1+1)=6.
=2(2×1+1)=6.
Электроны с l =2 называются d-электронами: 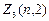 =2(2 2+1)=10.
=2(2 2+1)=10.
Электроны с l=3 называются f-электронами: 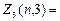 2(2×3+1)=14 и т.д.
2(2×3+1)=14 и т.д.
Максимальное число 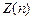 электронов, находящихся в состояниях, определяемых значением n главного квантового числа
электронов, находящихся в состояниях, определяемых значением n главного квантового числа 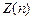 =
= 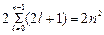 .
.
| Главное квантовое число | Электронная оболочка (слой) | Число электронов в состояниях | Максимальное число электронов | |||
s
( 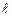 =0) =0)
| p
( 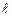 =1) =1)
| d
( 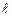 =2) =2)
| f
( 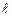 =3) =3)
| |||
| K | – | – | – | |||
| L | – | – | ||||
| M | – | |||||
| N |
Электроны, занимающие совокупность состояний с одинаковым значением главного квантового числа n, образуют электронные слои: К-слой при n = 1; L-слой при n = 2; M-слой при n = 3; N-слой при n =4 и т.д. В каждой квантовой оболочке атома электроны распределяются по подоболочкам, соответствующим определенному значению орбитального квантового числа 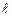 ; в зависимости от
; в зависимости от 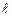 электрон находится в подгруппе с символами s, p, d, f и т.д.
электрон находится в подгруппе с символами s, p, d, f и т.д.
Таблица Менделеева. Характеристическое рентгеновское излучение.
В 1869 г. Д.И.Менделеев создал периодическую систему элементов. Он показал, что если элементы расположены по порядку возрастных атомных весов за некоторым исключением, то их физические и химические свойства периодически повторяются. По теории Бора такая периодичность в свойствах элементов объясняется тем, что электроны в атомах располагаются по определенным слоям и оболочкам. Электроны, входящие в состав одного слоя, имеют одно и то же главное квантовое число. Оказалось, что каждый период таблицы Менделеева начинается с заполнения электронами нового слоя. Физико-химические свойства элементов (валентность) и оптические свойства определяются числом и расположением самых внешних валентных электронов.
Проследим построение периодической системы (или заполнение электронами слоев атома), которые подчиняются двум принципам: а) заполнение начинается с наименьшей энергии (наиболее устойчивое состояние); б) принцип запрета Паули.
Первый элемент в таблице Менделеева – атом водорода Н, для него Z = 1. Он имеет один электрон, квантовые числа для которого: n =1, 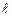 = 0, mе = 0, ms = +1/2 или –1/2, т. е. электронная конфигурация атома водорода: 1S1.
= 0, mе = 0, ms = +1/2 или –1/2, т. е. электронная конфигурация атома водорода: 1S1.
У следующего элемента гелия Не имеются два электрона, квантовые числа: n =1, 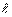 = 0, mе = 0, ms = ±1/2, т. е. электронная конфигурация атома гелия: 1S2. Слой К с числом электронов N = 2 заполнен полностью.
= 0, mе = 0, ms = ±1/2, т. е. электронная конфигурация атома гелия: 1S2. Слой К с числом электронов N = 2 заполнен полностью.
Третий элемент литий Li. Его третий электрон имеет квантовые числа: n = 2, 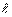 = 0, mе = 0, ms = +1/2 или – 1/2, т. е. электронная конфигурация атома 1S2 2S1.
= 0, mе = 0, ms = +1/2 или – 1/2, т. е. электронная конфигурация атома 1S2 2S1.
У берилия Ве: Z = 4 электронная конфигурация атома 1S2 2S2.
У последующих шести элементов происходит заполнение оболочек 2р. В результате у неона Nе с Z = 10 электронная конфигурация атома 1S2 2S2 2Р6, т.е. L – слой полностью заполнен и на этом заканчивается второй слой периодической таблицы. Не, Nе, а также другие атомы, в которых s- или s- и p-подгруппы полностью заняты электронами, по свойствам аналогичны и химически инертны. У последующих 6-ти элементов происходит заполнение оболочек 2р. В результате у неона Ne с Z=10 --1S22S22P6, т.е.L слой полностью заполнен и на этом заканчивается 2-ой слой периодической таблицы. Не, Nе по свойствам аналогичны.
| Z | символ элемента | Название элемента | Электронная конфигурация |
| Н | водород | 1s1 | |
| Не | гелий | 1s2 | |
| Li | литий | 1s2 2s1 | |
| Be | бериллий | 1s22s2 | |
| B | бор | 1s22s22p1 | |
| C | углерод | 1s22s22p2 | |
| N | азот | 1s22s22p3 | |
| O | кислород | 1s22s22p4 | |
| F | фтор | 1s22s22p5 | |
| Ne | неон | 1s22s22p6 |
Нарушения при заполнении слоев наблюдаются с Z=16 (К-калий), где начинает заполняться оболочка 4S при незаполненной 3d и еще у редкоземельных элементов заполнены оболочки: 5S, 5p, 6S при незаполненной 4f оболочке. Объясняется это тем, что они энергетически выше, чем заполняемые.
Экспериментально определить распределение электронов по оболочкам можно по спектрам рентгеновского излучения, длины волн которого лежат в диапазоне от 8.10–8 до 10–12 м. Различают тормозное и характеристическое рентгеновское излучение. Тормозное рентгеновское излучение возникает в результате торможения быстрых электронов и имеет сплошной непрерывный спектр, ограниченный со стороны малых длин волн границей. Характеристическое рентгеновское излучение возникает при торможении электронов больших энергий и имеет линейчатый спектр. Оно возникает в результате вырывания электрона с одной из близких к ядру слоев атома(К, L, М). На освободившееся место переходит электрон атома из более удаленной от ядра оболочки. Этот переход сопровождается испусканием кванта рентгеновского излучения энергией 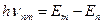 , частота которого определяется зарядом ядра Ze, квантовыми числами оболочек, между которыми совершается переход. Поэтому спектр, характерный рентгеновскому излучению, линейчатый.
, частота которого определяется зарядом ядра Ze, квантовыми числами оболочек, между которыми совершается переход. Поэтому спектр, характерный рентгеновскому излучению, линейчатый.

Г.Мозли в 1913 установил, что частоты характеристического спектра элементов возрастают с увеличением порядкового номера: 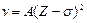 (А – постоянная). Длины волн в спектре характеристического рентгеновского излучения можно определить по закону Мозли:
(А – постоянная). Длины волн в спектре характеристического рентгеновского излучения можно определить по закону Мозли: 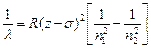 ,
,
где R – постоянная Ридберга, 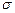 – постоянная экранирования; n1=1,2,3,… (определяет рентгеновскую серию), n2 принимает целочисленные значения, начиная с n1+1 (определяет отдельную линию соответствующей серии).
– постоянная экранирования; n1=1,2,3,… (определяет рентгеновскую серию), n2 принимает целочисленные значения, начиная с n1+1 (определяет отдельную линию соответствующей серии).
Смысл постоянной экранирования 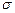 заключается в том, что на электрон, совершающий переход, соответствующий некоторой линии, действует не весь заряд ядра Ze, а заряд (Z–s)e, ослабленный экранирующим действием других электронов.
заключается в том, что на электрон, совершающий переход, соответствующий некоторой линии, действует не весь заряд ядра Ze, а заряд (Z–s)e, ослабленный экранирующим действием других электронов.
Например, для Кa-линии 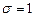 , и закон Мозли запишется в виде:
, и закон Мозли запишется в виде: 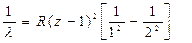 .
.
В L-серии для линии La 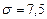 , тогда закон Мозли:
, тогда закон Мозли: 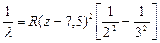 .
.
Дата добавления: 2015-08-08; просмотров: 5258;
