Спектральные серии атома водорода
Атомы, в виде разреженного газа или паров металла, дают спектр излучения, состоящий из отдельных линий. Такие спектры называются линейчатыми. При этом линии в спектре можно объединить в группы или в серии.
Особенно отчетливо это проявляется в спектре простейшего атома водорода.
Швейцарский физик Бальмер показал, что длины волн 4-х линий в видимой области спектра водорода можно определять по общей формуле:
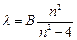 (6.1),
(6.1),
В=const, n=3;4;5;6.
Если введем обозначение vў = 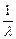 - волновое число, тогда:
- волновое число, тогда:
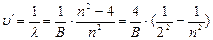 (6.2),
(6.2),
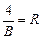 - постоянная Ридберга.
- постоянная Ридберга.
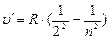 , серия, Бальмера, n = 3;4;5;6 (6.3)
, серия, Бальмера, n = 3;4;5;6 (6.3)
Волновые числа 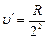 (при n ®Ґ),
(при n ®Ґ), 
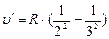 определяют границы спектральной серии.
определяют границы спектральной серии.
Наряду с серией Бальмера в спектре атомарного водорода были обнаружены другие серии, волновые числа которых можно представить аналогичными формулами.
В ультрафиолетовой области серия Лаймана:
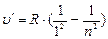 n = 2;3… (6.4),
n = 2;3… (6.4),
В инфракрасной области:
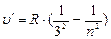 - серия Пашена, n =4;5…
- серия Пашена, n =4;5…
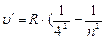 ) - серия Брэкета, n = 5;6… (6.5)
) - серия Брэкета, n = 5;6… (6.5)
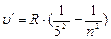 - серия Пфунда, n = 6;7…
- серия Пфунда, n = 6;7…
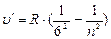 - серия Хемфри, n = 7;8…
- серия Хемфри, n = 7;8…
Анализируя соотношения (6.3) – (6.5), можно сказать, что все серии атомарного водорода можно представить общей формулой:
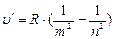 (6.6) – обобщенная формула Бальмера:
(6.6) – обобщенная формула Бальмера:
m=1;2;3;4;5;6; n=m+1, m+2,…
Обозначим величины 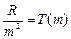 и
и 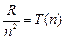 - спектральные термы.
- спектральные термы.
Тогда (6.6) запишется 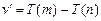 (6.7).
(6.7).
Соотношение (6.7) получило название комбинационный принцип.
Этот принцип был установлен опытным путем, а теория Бора дала ему толкование: Каждому спектральному терму соответствует определенное стационарное состояние атома и 2–ой постулат Бора – это есть комбинационный принцип, выраженный иным способом. Действительно, т.к. 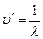 , а
, а 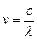 , то
, то 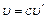 . По II постулату Бора
. По II постулату Бора 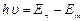 или
или 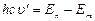 ,
, 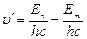 (6.8).
(6.8).
Сравнивая (6.7) и (6.8) можно записать: 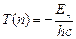 и
и  . Отсюда получается:
. Отсюда получается: 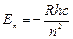 (6.9)
(6.9)
– энергия стационарного состояния атома. Знак «-» имеет условное значение, чисто физический смысл – энергия электрона в поле положительного ядра отрицательна.
Из (6.9) видно, что энергия стационарных состояний образует дискретный ряд при n=1;2;3…
§ 7. Теория атома водорода по Бору
По модели Резерфорда атом водорода: имеет в центре положительно заряженное ядро – протон, вокруг движется электрон.
Потенциальная энергия взаимодействия электрона с ядром:
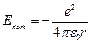 (7.1), r – радиус орбиты.
(7.1), r – радиус орбиты.
Кинетическая энергия электрона, движущего вокруг ядра: 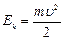 (7.2).
(7.2).
Тогда полная энергия атома: 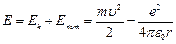 (7.3).
(7.3).
Электрон вокруг ядра движется с ускорением под действием Кулоновской силы, которые определяются как 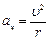 ;
; 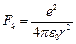 .
.
По II закону Ньютона (ma = Fk) можно записать: 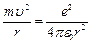 (7.4);
(7.4);
отсюда 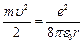 (7.5).Поставим (7.5) в (7.3) и получим выражение для полной энергии
(7.5).Поставим (7.5) в (7.3) и получим выражение для полной энергии
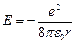 (7.6).
(7.6).
По классической механике радиус орбиты электрона может принимать любые значения, тогда и энергия согласно (7.6) может принимать любые значения. Согласно постулатам Бора энергия атома, а значит и радиус орбиты электрона определенные. Бор предложил правило отбора или правило квантования (III постулат Бора).
Из всех возможных орбит электрона осуществляется только те, для которых момент импульса электрона кратен постоянной Планка: 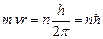 (7.7), где n=1,2,3,… - главное квантовое число.
(7.7), где n=1,2,3,… - главное квантовое число.
Решим систему уравнений:
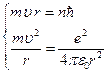
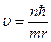 подставим во вторую формулу системы:
подставим во вторую формулу системы: 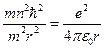
определим радиус стационарной орбиты электрона:
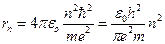 (7.8),
(7.8),
при 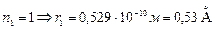 (радиус 1-ой орбиты).
(радиус 1-ой орбиты).
Из (7.8) 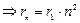 . Подставляя rn из (7.8) в выражение для энергии
. Подставляя rn из (7.8) в выражение для энергии 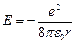
получим:
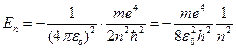 (7.9)
(7.9)
Дата добавления: 2015-08-08; просмотров: 1845;
