Неравновесные процессы

Вследствие необратимости термодинамических процессов все процессы в изолированной системе протекают лишь в одном направлении — в направлении приближения системы к состоянию теплового равновесия. Будучи выведена из состояния равновесия, система переходит в новое состояние равновесия спустя некоторое время — время релаксации. Оно зависит от температуры, давления, плотности системы, а также от характера взаимодействия между частицами. Переход системы к равновесному состоянию представляет собой необратимый процесс, поскольку вероятность самопроизвольного перехода равновесной системы в неравновесное состояние ничтожно мала.

Рассмотрим некоторые механизмы неравновесной релаксации системы к состоянию равновесия. Прежде всего, введем понятие длины свободного пробега молекул. Индивидуальные особенности движения отдельных молекул не играют роли в системе большого числа частиц, поэтому под длиной свободного пробега l понимают среднюю длину пути молекулы в газе между столкновениями. Поскольку столкновения носят случайный характер, длина свободного пробега имеет вероятностный смысл: величина l тем меньше, чем больше вероятность столкновения молекул. В свою очередь, вероятность столкновения молекул определяется их плотностью и размерами молекул. Наряду с длиной свободного пробега другой важной характеристикой является среднее время свободного пробега

t = l/v, (2.46)

где v — средняя скорость теплового движения молекул. Обе введенные здесь величины в существенной степени определяют скорость релаксационного процесса.

Механизм процесса релаксации состоит в том, что при выведении системы из состояния равновесия в газе возникает поток соответствующей величины: тепла, массы, концентрации частиц в зависимости от того, каким способом система была выведена из состояния равновесия. При приближении системы к равновесию этот поток исчезает, перераспределяясь по всей системе.

Определим поток произвольной физической величины как изменение этой величины в единицу времени в какой-либо точке пространства

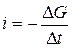, (2.47)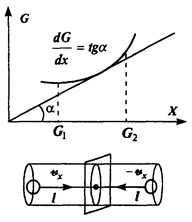

где ΔG — разность значения величины G в соседние моменты времени. Знак минус означает, что направление потока противоположно направлению возрастания величины. Само по себе изменение величины G не зависит от времени явно, а связано с ее неоднородным распределением в пространстве, например, вдоль оси X (см. рис.). Поэтому перепишем выражение для потока в виде: .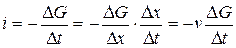

При получении формулы для полного потока это выражение нужно умножить на число частиц — носителей величины G, которые в состоянии пересечь в единицу времени единичную площадку, перпендикулярную оси X. Число таких частиц равно числу частиц, движущихся параллельно оси X и отстоящих от указанной площадки на расстояние, не большее длины свободного пробега l, т. е. заключенных в объеме, основание которого едини­ца, а длина равна 2l. Число частиц в единице объема» движущихся в направлении оси X, равно n/6 и (ввиду равновероятности движения в любом из возможных шести направлений). Полный поток величины G равен

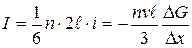. (2.48)

Величина 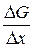представляет собой градиент G в направлении оси X. Таким образом, если в системе имеется неоднородное распределение какой-либо физической величины, то возникает поток этой величины, обусловленный столкновением частиц и пропорциональный ее rwl градиенту. Величина nvl/3 коэффициент переноса.

Рассмотрим конкретные процессы переноса.

Теплопроводность. Пусть системе сообщено некоторое количество тепла. При этом некоторая часть системы оказывается более нагретой, откуда тепло посредством столкновений распространяется по всему объему, т. е. возникает поток тепла. Переносимая физическая величина в этом случае — тепло, значит G = Q. Поскольку количество тепла характеризуется температурой Q = C_VT , где С_V — теплоемкость вещества, то, подставляя вместо G в общую формулу (2.48) это выражение, получим: .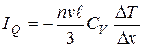

Следовательно, поток тепла пропорционален градиенту температуры. Величина 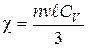‑ коэффициент теплопроводности.

Диффузия. Если в систему добавляется некоторое количество частиц того или другого сорта, то в объеме возникает неоднородное распределение концентрации этих частиц и в силу указанных причин возникает поток концентрации этих частиц. Роль величины G играет относительная концентрация добавленных частиц G = n'/n. Процесс выравнивания концентраций, обусловленный механизмом столкновений, называется диффузией. Выражение для диффузионного потока, согласно (2.48), принимает вид:

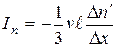, (2.50)

где коэффициент между потоком и градиентом концентрации представляет собой коэффициент диффузии D = vl/3.

Вязкость. Предположим, что нам удалось механическим или иным способом сообщить механический импульс какой-либо части нашей системы. Тем самым в системе создается направленный поток частиц и распределение импульса частиц в плоскости, перпендикулярной потоку, становится неоднородным. Благодаря столкновениям частиц, происходит передача импульса направленного движения окружающим частицам, в результате чего возникает перераспределение переданного импульса. Этот процесс, который можно рассматривать как диффузию в пространстве импульсов, называется вязкостью, или внутренним трением. Переносимой величиной является импульс частицы, который мы обозначим здесь через mu; u обозначает здесь направленную скорость частиц в отличие от тепловой скорости. Поток импульса

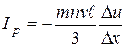, (2.51)

а коэффициент вязкости среды v = nvnl/3 = pvl/3.