Тепловые машины

Термодинамика как наука развилась в начале XIX века из необходимости объяснить работу тепловых машин. Термодинамические расчеты необходимы при конструировании любых машин, способных производить работу. Тепловой машиной называется устройство, использующее тепловую энергию для совершения механической работы. В этом смысле и паровой двигатель, и атомный реактор эквивалентны.

Тепловая машина состоит из нагревателя, рабочего тела и охладителя рабочего тела. Охладителем, в конечном счете, служит окружающая среда. Тепловая машина работает по принципу замкнутого цикла, совершая круговой процесс. В ходе прямого цикла рабочее тело, например, пар, получив от нагревателя количество тепла Q₁, расширяется от объема V₁ до объема V₃. Согласно первому закону термодинамики, это тепло расходуется на нагревание рабочего тела и на совершение механической работы

Q₁ = E₂ ‑ E₁ + A₁₃, (2.52)

где E₂ ‑ E₁ — изменение внутренней энергии рабочего тела при переходе из состояния 1 в состояние 3. При обратном цикле над газом производится работа: газ сжимается и передает охладителю количество тепла

‑ Q₂ = E₁ ‑ E₂ + A₃₁. (2.53)

Складывая оба уравнения, получим Q₁ ‑ Q₂ = A₁₃ + A₃₁ =A, где А — полная работа, совершенная машиной за один цикл.

Отношение полезной работы, совершенной машиной, к количеству полученного тепла составляет КПД тепловой машины

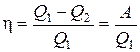. (2.54)

Понятно, что КПД машины всегда меньше единицы, поскольку не все количество полученного тепла переходит в полезную работу.

В реальных тепловых машинах КПД, очевидно, еще меньше, так как часть тепла теряется безвозвратно в процессе работы машины. Для получения максимального КПД следует рассмотреть рабочий цикл, образованный обратимыми процессами. Этому требованию отвечает цикл (см. рис.), впервые рассмотренный французским ученым Карно. В качестве рабочего тела в цикле Карно рассматривается идеальный газ. Цикл Карно состоит из последовательных расширения и сжатия газа, причем каждый из процессов совершается сначала изотермически, а затем адиабатически. При прямом цикле тело по-прежнему сначала получает тепло, а затем отдает его. Достоинство цикла Карно состоит в том, что все процессы обратимы, и, следовательно, КПД такой машины будет максимальным.

Пусть газ расширяется изотермически, переходя из состояния 1 в состояние 2. При изотермическом процессе внутренняя энергия газа не изменяется, и количество полученного тепла Q₁ равно работе А₁₂. По формуле (2.38):

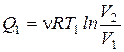. (2.55)

На участке 2-3 газ расширяется адиабатически. На участке 3‑4 он сжимается опять изотермически, для чего охладителю должно быть отдано тепло Q₂. Работа на участке 3‑4 равна ‑ Q₂, причем

. (2.56)

Наконец, на участке 4‑1 газ адиабатически сжимается, возвращаясь к исходному состоянию. Воспользуемся уравнением адиабаты (2.42), заменив в нем, согласно уравнению состояния PV , на ν·RT. Уравнение адиабаты принимает вид:

TV ^γ‑1 = const. (2.57)

Для процессов 2‑3 и 4‑1 цикла Карно отсюда следует:

.

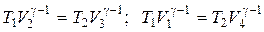Разделив первое уравнение на второе, получим V₂/V₁ = V₃/V₄. После подстановки этого выражения в (2.56) найдем:

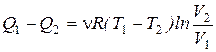. (2.58)

Подставляя (2.58) в формулу (2.54), получим выражение для КПД цикла Карно:

. (2.59)

Из формулы (2.59) следует, что КПД тепловой машины определяется только разностью температур нагревателя и холодильника. КПД не зависит ни от свойств рабочего тела, используемого в машине, ни от свойств самой машины. Полученный результат показывает, что при T₁ = T₂ КПД машины равен нулю, т. е. машина не совершает работы. Работа максимальна (η = 1) при T₂ = 0. Таким образом, машина тем выгоднее, чем ниже температура охладителя.