Обратимые и необратимые процессы. Новой качественной особенностью систем большого числа частиц по сравнению с чисто механическими системами является необратимый характер термодинамических

Новой качественной особенностью систем большого числа частиц по сравнению с чисто механическими системами является необратимый характер термодинамических процессов. Если рассматривать движение тела как механический процесс, в результате которого происходит изменение его координат и скоростей, то очевидно, что в механике без учета сил трения все процессы обратимы. Обратимость механического процесса означает, что если изменить направление процесса на обратное, то тело, обладающее определенными значениями координат и скорости в конечном состояний, будет проходить последовательность тех же состояний, которую оно проходило при первоначальном направлении процесса, но в обратном порядке и в конце процесса окажется опять в состоянии с начальными значениями координат и скорости. Таково, например, упругое столкновение шаров, которое может происходить как в прямом, так и в обратном направлениях. Этот факт — прямое следствие второго закона Ньютона, сохраняющего постоянной полную механическую энергию системы. Запишем его в форме

.

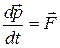Второй закон Ньютона представляет собой уравнения движения тела. Решив эти уравнения относительно координат и импульса как функций времени, можно определить с достоверностью их значения в любой последующий момент времени, если известны значения этих величин в начальный момент: r(0) и p(0). С такой же достоверностью можно, пользуясь уравнениями Ньютона, проследить за движением тела в обратном направлении. Если заменить в законе Ньютона t на - t и p на - p , то уравнения движения не изменятся. Это означает, что если известны координаты и скорости тела в конечном состоянии, можно определить их значения в любой заданный момент в прошлом. Таким образом, задание начальных или конечных условий полностью определяет поведение механической системы в будущем или в прошлом.

Иная ситуация возникает в системах, состоящих из большого числа частиц. Каждая частица в отдельности, конечно, по-прежнему подчиняется уравнениям движения в форме второго закона Ньютона. Отличие состоит в том, что в системе большого числа частиц каждая отдельная частица испытывает большое число последовательных столкновений с другими частицами. Поскольку столкновения имеют случайный характер и изменяют координаты и скорости данной частицы непредсказуемым образом, то информацию о состоянии данной частицы по прошествии некоторого времени в системе большого числа частиц можно теперь определить не с достоверностью, как в механике, а только с некоторой вероятностью. Поскольку всякий термодинамический процесс включает в себя множество независимых случайных событий, то для того, чтобы он мог происходить в обратном направлении, необходимо, чтобы реализовалась вся эта случайная последовательность событий в обратном порядке. Поскольку вероятность нескольких независимых событий есть произведение вероятностей каждого из событий, то суммарная вероятность обратного процесса оказывается ничтожно малой, практически равной нулю. В качестве примера такого процесса укажем на процесс передачи тепла от более нагретого тела менее нагретому —обратный процесс, как известно, сам но себе никогда не реализуется на практике. Таким образом, физическая причина необратимости термодинамических процессов заключается в случайном характере столкновений частиц, который создает неопределенность в начальных условиях к уравнениям движения частиц.

Реальный термодинамический процесс всегда необратим. Тем не менее в термодинамике говорят об обратимом процессе как о некоторой идеализированной схеме процесса. Рассмотрим некоторый равновесный процесс, совершаемый системой под влиянием внешнего воздействия так, что система последовательно проходит через ряд равновесных состояний из начального в конечное. Если ту же последовательность состояний можно реализовать в обратном порядке и при этом не изменить состояния окружающих тел, то процесс будет обратимым. При этом каждая из частиц системы вовсе не вернется в свое исходное состояние, важно только, что средние, равновесные характеристики системы примут свои начальные значения, а это происходит при обратимом процессе благодаря неразличимости или тождественности частиц системы.