Уравнение непрерывности. Закон сохранения заряда, условие стационарности (постоянства) тока.
 Уравнение непрерывности как раз соответствует закону сохранения заряда, имеется в виду следующее равенство:
Уравнение непрерывности как раз соответствует закону сохранения заряда, имеется в виду следующее равенство:
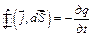 ,
,
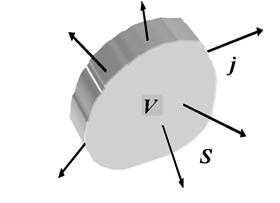
где в левой части уравнения – заряд, вышедший за единицу времени за пределы объема V через замкнутую поверхность S, ограничивающую этот объем, в правой – убыль заряда в единицу времени внутри этого объема, эта величина показывает, как быстро изменяется заряд, находящийся внутри объема. Значки частной производной в правой части уравнения означают, что мы вычисляем поток по области с фиксированными границами. Так как слева стоит величина положительная, выражение справа тоже должно быть положительно, но у нас заряд со временем убывает, поэтому мы и ставим перед частной производной заряда по времени знак минус.
Дифференциальная форма закона сохранения заряда будет иметь вид:
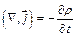
Вообще для всех интегральных и локальных связей характерно, что интегральная связь ставит в соответствие, допустим, заряд внутри заданного объема и ток в другой точке пространства, например, в точках некоторой поверхности, а в дифференциальной связи 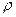 - объемная плотность заряда в той же точке пространства, где и вектор
- объемная плотность заряда в той же точке пространства, где и вектор 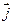 .
.
Если ток постоянный, то заряд внутри выделенного замкнутого объема не изменяется, тогда
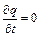 , а значит и
, а значит и  .
.
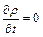 , а значит и
, а значит и 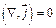 .
.
Дата добавления: 2015-08-08; просмотров: 1033;
